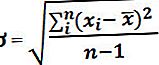ন্যূনতম স্কোয়ারস রিগ্রেশন - সেরা ফিটের লাইন কীভাবে তৈরি করবেন?
সর্বনিম্ন স্কোয়ারগুলি রিগ্রেশন পদ্ধতির সংজ্ঞা
একটি সর্বনিম্ন-স্কোয়ারের রিগ্রেশন পদ্ধতি হ'ল একধরণের রেগ্রেশন বিশ্লেষণ যা লিনিয়ার লাইনের সাথে নির্ভরশীল এবং স্বতন্ত্র ভেরিয়েবলের মধ্যে সম্পর্ক স্থাপন করে। এই লাইনটিকে "সেরা ফিটের লাইন" হিসাবে উল্লেখ করা হয়।
রিগ্রেশন অ্যানালাইসিস হ'ল একটি পরিসংখ্যানগত পদ্ধতি যার সাহায্যে একজন অন্য ভেরিয়েবলের জ্ঞাত মানগুলি থেকে একটি ভেরিয়েবলের অজানা মানগুলি অনুমান বা ভবিষ্যদ্বাণী করতে পারে। পরিবর্তনশীল সুদের পূর্বাভাস দেওয়ার জন্য যে ভেরিয়েবলটি ব্যবহৃত হয় তাকে স্বাধীন বা ব্যাখ্যামূলক ভেরিয়েবল বলা হয় এবং যে ভেরিয়েবলের পূর্বাভাস দেওয়া হয় তাকে নির্ভরশীল বা ব্যাখ্যাযোগ্য ভেরিয়েবল বলা হয়।
আসুন x এবং y দুটি ভেরিয়েবল বিবেচনা করি। এগুলি একটি গ্রাফে y- অক্ষের y- এর x- অক্ষের মানগুলির সাথে একটি গ্রাফে প্লট করা হয়। এই মানগুলি নীচের গ্রাফের বিন্দু দ্বারা প্রতিনিধিত্ব করা হয়। বিন্দুর মধ্য দিয়ে একটি সরল রেখা আঁকা - সেরা ফিটের রেখা হিসাবে উল্লেখ করা হয়।

সর্বনিম্ন স্কোয়ার রিগ্রেশনের উদ্দেশ্য হ'ল নিশ্চিত করা যে প্রদত্ত মানগুলির সেটের মধ্য দিয়ে আঁকা রেখাটি মানগুলির মধ্যে নিকটতম সম্পর্ক স্থাপন করে।
সর্বনিম্ন স্কোয়ারগুলির রিগ্রেশন সূত্র
নিম্নতম স্কোয়ার পদ্ধতির অধীনে রিগ্রেশন রেখাটি নিম্নলিখিত সূত্রটি ব্যবহার করে গণনা করা হয় -
ŷ = এ + বিএক্স
কোথায়,
- dependent = নির্ভরশীল পরিবর্তনশীল
- x = স্বতন্ত্র পরিবর্তনশীল
- a = y-intercep
- b = লাইনের opeাল
নীচের সূত্রটি ব্যবহার করে লাইনের খের slাল গণনা করা হয় -

বা

ওয়াই-ইন্টারসেপ্ট, ‘এ’ নিম্নলিখিত সূত্র ব্যবহার করে গণনা করা হয় -

সর্বনিম্ন স্কোয়ার রিগ্রেশন-এ সেরা ফিটের লাইন
সেরা ফিটের লাইনটি এমন একটি সরল রেখা যা ডেটার পয়েন্টগুলির বিচ্ছুরণের মধ্য দিয়ে আঁকানো হয় যা তাদের মধ্যে সম্পর্কের পক্ষে সর্বোত্তমভাবে প্রতিনিধিত্ব করে।
আসুন নীচের গ্রাফটি বিবেচনা করুন যেখানে x এবং y- অক্ষের সাথে ডেটার একটি সেট প্লট করা হয়েছে। এই ডেটা পয়েন্টগুলি নীল বিন্দু ব্যবহার করে প্রতিনিধিত্ব করা হয়। এই পয়েন্টগুলির মাধ্যমে তিনটি লাইন আঁকা - একটি সবুজ, একটি লাল এবং নীল রেখা। সবুজ রেখাটি একটি বিন্দু দিয়ে যায় এবং লাল রেখাটি তিনটি ডাটা পয়েন্টের মধ্য দিয়ে যায়। তবে নীল রেখাটি চারটি ডাটা পয়েন্টের মধ্য দিয়ে যায় এবং অন্যান্য দুটি লাইনের তুলনায় নীল লাইনের অবশিষ্টাংশগুলির মধ্যবর্তী দূরত্বটি ন্যূনতম হয়।

উপরের গ্রাফে, নীল রেখাটি সেরা মানানসই রেখাকে উপস্থাপন করে কারণ এটি সমস্ত মানের সাথে সবচেয়ে কাছাকাছি অবস্থিত এবং রেখার বাইরে লাইনের পয়েন্টগুলির মধ্যে দূরত্ব ন্যূনতম (যেমন সেরা ফিটের রেখার অবশিষ্টাংশগুলির মধ্যে দূরত্ব - অবশিষ্টাংশের বর্গের যোগফল হিসাবেও উল্লেখ করা হয়)। অন্যান্য দুটি লাইনে কমলা এবং সবুজ, নীল রেখার তুলনায় রেখাগুলির অবশিষ্টাংশের মধ্যে দূরত্ব বেশি।
সর্বনিম্ন-স্কোয়ার পদ্ধতিটি অবশিষ্টাংশ এবং সেরা ফিটের রেখার মধ্যবর্তী দূরত্ব হ্রাস করে নির্ভরশীল এবং স্বতন্ত্র পরিবর্তনশীলগুলির মধ্যে নিকটতম সম্পর্ক সরবরাহ করে অর্থাত্ অবশিষ্টাংশের বর্গের যোগফল এই পদ্ধতির অধীনে ন্যূনতম। সুতরাং এই শব্দটি "ন্যূনতম স্কোয়ার"
সর্বনিম্ন স্কোয়ারগুলি রিগ্রেশন লাইনের উদাহরণ
আসুন নীচের প্রশ্নে এই সূত্রগুলি প্রয়োগ করুন -
আপনি এই সর্বনিম্ন স্কোয়ারগুলি রিগ্রেশন এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - ন্যূনতম স্কোয়ারগুলি রিগ্রেশন এক্সেল টেম্পলেটউদাহরণ # 1
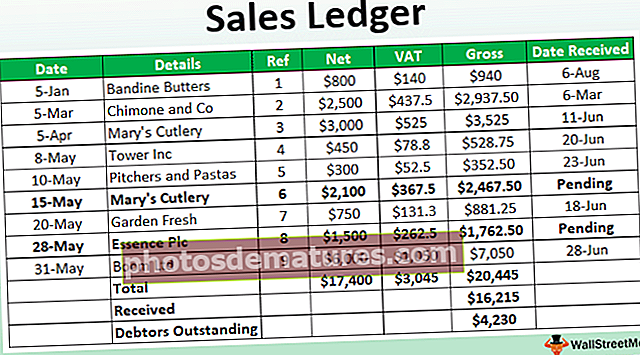
কোনও সংস্থায় প্রযুক্তিবিদদের অভিজ্ঞতার সাথে সম্পর্কিত বিশদ (বহু বছর ধরে) এবং তাদের পারফরম্যান্স রেটিং নীচের সারণিতে সরবরাহ করা হয়েছে। এই মানগুলি ব্যবহার করে, 20 বছরের অভিজ্ঞতার সাথে কোনও প্রযুক্তিবিদের জন্য পারফরম্যান্স রেটিংয়ের অনুমান করুন।

সমাধান -
সর্বনিম্ন বর্গক্ষেত্র গণনা করতে আমরা প্রথমে Y- ইন্টারসেপ্ট (ক) এবং একটি লাইনের bাল (খ) গণনা করব -

লাইনের bাল (খ)

- খ = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
- = 247/218
- = 1.13
ওয়াই-ইন্টারসেপ্ট (ক)

- a = 648 - (1.13) (80) / 8
- = 69.7
নিগ্রহের রেখাটি নিম্নরূপ গণনা করা হয় -

সূত্রটিতে x এর মানের জন্য 20 প্রতিস্থাপন,
- ŷ = এ + বিএক্স
- ŷ = 69.7 + (1.13) (20)
- ŷ = 92.3
20 বছরের অভিজ্ঞতার সাথে একজন প্রযুক্তিবিদের পারফরম্যান্স রেটিং 92.3.3 বলে অনুমান করা হয়।
উদাহরণ # 2
এক্সেল ব্যবহার করে স্বল্প স্কোয়ারগুলির রিগ্রেশন সমীকরণ
নিম্নোক্ত স্কোয়ারগুলির রিগ্রেশন সমীকরণটি নিম্নলিখিত পদক্ষেপগুলি দ্বারা এক্সেল ব্যবহার করে গণনা করা যেতে পারে -
- এক্সেলে ডেটা টেবিল .োকান।

- ডেটা পয়েন্টগুলি ব্যবহার করে একটি স্ক্যাটার গ্রাফ sertোকান।

- স্ক্যাটার গ্রাফের মধ্যে একটি ট্রেন্ডলাইন .োকান।

- ট্রেন্ডলাইন বিকল্পগুলির অধীনে - লিনিয়ার ট্রেন্ডলাইন নির্বাচন করুন এবং চার্টে প্রদর্শন সমীকরণ নির্বাচন করুন।

- এক্সেল ডেটা প্রদত্ত সেটটির জন্য সর্বনিম্ন-স্কোয়ারগুলির রিগ্রেশন সমীকরণ চার্টে প্রদর্শিত হয়।

সুতরাং, এক্সেল ডেটার প্রদত্ত সেটটির জন্য সর্বনিম্ন-স্কোয়ারগুলির রিগ্রেশন সমীকরণ গণনা করা হয়। সমীকরণটি ব্যবহার করে, পূর্বাভাস এবং প্রবণতা বিশ্লেষণ করা যেতে পারে। এক্সেল সরঞ্জামগুলি বিশদ প্রতিরোধের গণনার জন্য সরবরাহ করে।
সুবিধাদি
- রিগ্রেশন বিশ্লেষণের সর্বনিম্ন-স্কোয়ার পদ্ধতিটি পূর্বাভাস মডেল এবং প্রবণতা বিশ্লেষণের জন্য সবচেয়ে উপযুক্ত। এটি অর্থনীতি, ফিনান্স এবং স্টক মার্কেটের ক্ষেত্রে সবচেয়ে ভাল ব্যবহৃত হয় যেখানে বিদ্যমান ভেরিয়েবলের সাহায্যে এবং একইর মধ্যে সম্পর্কের সাহায্যে ভবিষ্যতের যে কোনও ভেরিয়েবলের মান পূর্বাভাস দেওয়া হয়।
- সর্বনিম্ন-স্কোয়ার পদ্ধতিটি ভেরিয়েবলগুলির মধ্যে নিকটতম সম্পর্ক সরবরাহ করে। এই পদ্ধতির অধীনে সেরা ফিটের লাইনের সাথে স্কোয়ারের অবশিষ্টাংশের যোগফলের মধ্যে পার্থক্য হ'ল।
- গণনা প্রক্রিয়া সহজ এবং প্রয়োগ করা সহজ।
অসুবিধা
- সর্বনিম্ন-স্কোয়ার পদ্ধতিটি প্রদত্ত ভেরিয়েবলগুলির সেটের মধ্যে নিকটতম সম্পর্ক স্থাপনের উপর নির্ভর করে। গণনা প্রক্রিয়াটি ডেটাতে সংবেদনশীল এবং কোনও বহিরাগতের ক্ষেত্রে (ব্যতিক্রমী ডেটা) ফলাফলগুলি মূলত প্রভাবিত হতে পারে।
- এই জাতীয় গণনা লিনিয়ার মডেলগুলির জন্য সবচেয়ে উপযুক্ত। ননলাইনী সমীকরণের জন্য, আরও পরিগণিত গণনা পদ্ধতি প্রয়োগ করা হয়।
উপসংহার
পূর্বাভাস মডেল এবং প্রবণতা বিশ্লেষণের জন্য সর্বাধিক জনপ্রিয় পদ্ধতিগুলির মধ্যে ন্যূনতম স্কোয়ার পদ্ধতি। যথাযথভাবে গণনা করা হলে, এটি সেরা ফলাফল সরবরাহ করে।