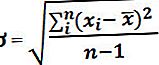নমুনা স্ট্যান্ডার্ড বিচ্যুতি সূত্র | কীভাবে গণনা করবেন?
নমুনা স্ট্যান্ডার্ড বিচ্যুতি গণনা করার সূত্র
নমুনা স্ট্যান্ডার্ড বিচ্যুতিটি পরিসংখ্যানীয় মেট্রিককে বোঝায় যা একটি নমুনার গড় থেকে যে পরিমাণ এলোমেলো পরিবর্তনশীলকে বিভক্ত করে এবং এটি গড় থেকে প্রতিটি ভেরিয়েবলের বিচ্যুতির স্কোয়ার যোগ করে গণনা করা হয়, তারপরে ফলাফলটি ভাগ করে বেশ কয়েকটি ভেরিয়েবল বিয়োগ এবং তারপরে ফলাফলের এক্সেলের মধ্যে বর্গমূলকে গণনা করা।
গাণিতিকভাবে, এটি হিসাবে উপস্থাপিত হয়,
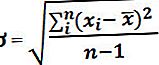
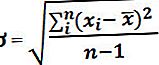
কোথায়
- এক্সi = ith এলোমেলো পরিবর্তনশীল
- এক্স = নমুনার গড়
- নমুনায় এন = ভেরিয়েবলের সংখ্যা
নমুনা স্ট্যান্ডার্ড বিচ্যুতি গণনা (ধাপে ধাপ)
- ধাপ 1: প্রথমত, বিশাল সংখ্যক ভেরিয়েবলের জনসংখ্যার থেকে এলোমেলো পরিবর্তনগুলি সংগ্রহ করুন gather এই পরিবর্তনগুলি একটি নমুনা গঠন করবে form ভেরিয়েবলগুলি x দ্বারা চিহ্নিত করা হয়i.
- ধাপ ২: এরপরে, নমুনায় ভেরিয়েবলের সংখ্যা নির্ধারণ করুন এবং এটি এন দ্বারা বোঝানো হয়েছে।
- ধাপ 3: এর পরে, সমস্ত এলোমেলো ভেরিয়েবল যুক্ত করে এবং নমুনায় ভেরিয়েবলের সংখ্যা দ্বারা ফলাফলকে ভাগ করে নমুনার গড়টি নির্ধারণ করুন। নমুনা গড়টি x দ্বারা চিহ্নিত করা হয়।
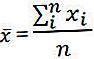
- পদক্ষেপ 4: এরপরে, নমুনার প্রতিটি ভেরিয়েবলের মধ্যে পার্থক্য গণনা করুন এবং নমুনার অর্থ অর্থাত xi - এক্স .
- পদক্ষেপ 5: এরপরে, সমস্ত বিচ্যুতির স্কোয়ার গণনা করুন (xi - এক্স) 2।
- পদক্ষেপ:: এরপরে, স্কোয়ারের সমস্ত বিচ্যুতিগুলি যুক্ত করুন ∑ (xi - এক্স) 2।
- পদক্ষেপ 7: এরপরে, সমস্ত বর্গাকার বিচ্যুতির সংখ্যাকে নমুনা বিয়োগ একে (এন - 1) এর ভেরিয়েবলের সংখ্যা দ্বারা ভাগ করুন।
- পদক্ষেপ 8: শেষ অবধি, নমুনা স্ট্যান্ডার্ড বিচ্যুতির সূত্রটি নিচের মত উল্লিখিত ফলাফলের বর্গমূলকে গণনা করে গণনা করা হয়।
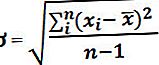
উদাহরণ
আপনি এই নমুনা স্ট্যান্ডার্ড বিচ্যুতি সূত্র এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - নমুনা স্ট্যান্ডার্ড বিচ্যুতি সূত্র এক্সেল টেম্পলেটউদাহরণ # 1
আসুন আমরা 5 জন শিক্ষার্থীর নমুনার উদাহরণটি গ্রহণ করি যারা প্রতি সপ্তাহে কতটি পেন্সিল ব্যবহার করছে তা দেখতে জরিপ করা হয়েছিল। তাদের দেওয়া প্রতিক্রিয়ার উপর ভিত্তি করে নমুনার স্ট্যান্ডার্ড বিচ্যুতি গণনা করুন: 3, 2, 5, 6, 4
দেওয়া,
- নমুনার আকার (এন) = 5
নীচে নমুনা স্ট্যান্ডার্ড বিচ্যুতি গণনার জন্য ডেটা দেওয়া আছে।
নমুনা গড়
নমুনা গড় গণনা
নমুনা গড় = (3 + 2 + 5 + 6 + 4) / 5

নমুনা গড় = 4
প্রতিটি ভেরিয়েবলের বিচ্যুতির স্কোয়ারগুলি নীচের হিসাবে গণনা করা যায়,
- (3 – 4)2 = 1
- (2 – 4)2 = 4
- (5 – 4)2 = 1
- (6 – 4)2 = 4
- (4 – 4)2 = 0
এখন, উপরের সূত্রটি ব্যবহার করে নমুনার স্ট্যান্ডার্ড বিচ্যুতি গণনা করা যেতে পারে,
- ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}
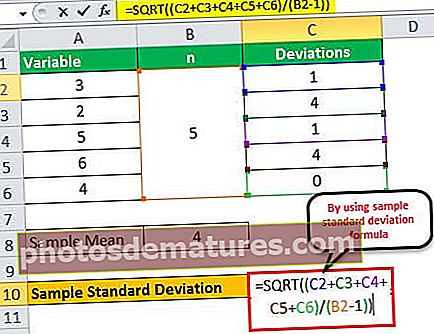
বিচ্যুতি হবে -
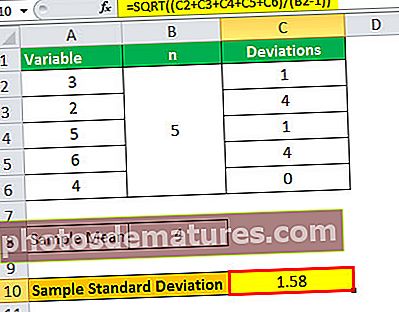
- ơ = 1.58
সুতরাং, নমুনার স্ট্যান্ডার্ড বিচ্যুতি 1.58।
উদাহরণ # 2
আসুন আমরা নিউইয়র্কের একটি অফিসের উদাহরণ নিই যেখানে কর্মরত জনসংখ্যার গড় বয়স নির্ধারণের জন্য প্রায় 5 হাজার লোক কাজ করে এবং 10 জনের একটি নমুনায় জরিপ চালানো হয়। প্রদত্ত 10 জনের বয়স অনুসারে নমুনা স্ট্যান্ডার্ড বিচ্যুতি নির্ধারণ করুন: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25
দেওয়া,
- নমুনা আকার (এন) = 10
উপরের ডেটা ব্যবহার করে আমরা প্রথমে নমুনা গড় গণনা করব
নমুনা গড়
নমুনা গড়ের গণনা
= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

নমুনা গড় = 27.8
প্রতিটি ভেরিয়েবলের বিচ্যুতির স্কোয়ারগুলি নীচের হিসাবে গণনা করা যায়,
- (23 – 27.8)2 = 23.04
- (27 – 27.8)2 = 0.64
- (33 – 27.8)2 = 27.04
- (28 – 27.8)2 = 0.04
- (21 – 27.8)2 = 46.24
- (24 – 27.8)2 = 14.44
- (36 – 27.8)2 = 67.24
- (32 – 27.8)2 = 17.64
- (29 – 27.8)2 = 1.44
- (25 – 27.8)2 = 7.84
বিচ্যুতি
উপরের সূত্রটি ব্যবহার করে এখন বিচ্যুতি গণনা করা যেতে পারে,
- ơ = √ {(23.04 + 0.64 + 27.04 + 0.04 + 46.24 +14.44 +67.24 + 17.64 + 1.44 + 7.84) / (10 - 1)}
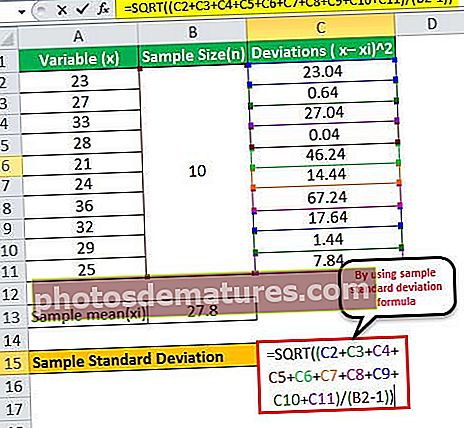
বিচ্যুতি হবে -
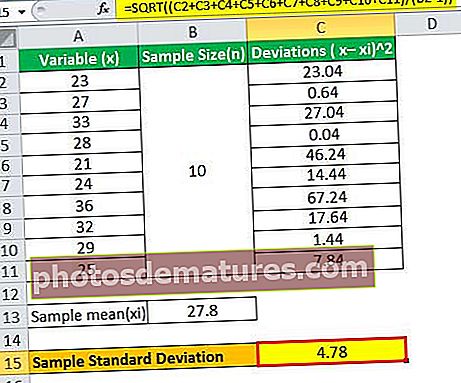
- ơ = 4.78
বিস্তারিত গণনা বুঝতে আপনি উপরে প্রদত্ত এক্সেল শিটটি উল্লেখ করতে পারেন।
প্রাসঙ্গিকতা এবং ব্যবহার
পরিসংখ্যানবিদদের দৃষ্টিকোণ থেকে নমুনা স্ট্যান্ডার্ড বিচ্যুতির ধারণাটি অত্যন্ত গুরুত্বপূর্ণ কারণ সাধারণত তথ্যের একটি নমুনা বড় আকারের ভেরিয়েবল (জনসংখ্যা) এর পুল থেকে নেওয়া হয় যার থেকে পরিসংখ্যানবিদরা সমগ্র জনগণের জন্য ফলাফলগুলি অনুমান বা সাধারণকরণের প্রত্যাশা করেন। স্ট্যান্ডার্ড বিচ্যুতির পরিমাপ এটি ব্যাতিক্রম নয় এবং তাই, পরিসংখ্যানবিদকে আঁকানো নমুনার ভিত্তিতে জনসংখ্যার মান বিচ্যুতির একটি মূল্যায়ন করতে হবে এবং এই কারণেই এই জাতীয় বিচ্যুতি কার্যকর হয়।