photosdematures.com

এক্সেল সহ চি-স্কয়ার টেস্ট

এক্সেল-এ চি-স্কোয়ার পরীক্ষাটি এলোমেলোভাবে নির্বাচিত তথ্যের জন্য দুই বা ততোধিক ভেরিয়েবলের তুলনা করতে ব্যবহৃত হয় সর্বাধিক ব্যবহৃত নন-প্যারাম্যাট্রিক পরীক্ষা। এটি এক ধরণের পরীক্ষা যা দুটি বা ততোধিক ভেরিয়েবলের মধ্যে সম্পর্ক সন্ধান করার জন্য ব্যবহৃত হয়, এটি পরিসংখ্যানগুলিতে ব্যবহৃত হয় যা চি-স্কোয়ার পি-মান হিসাবেও পরিচিত, এক্সেলে আমাদের একটি ইনবিল্ট ফাংশন নেই তবে আমরা ব্যবহার করতে পারি চি-স্কোয়ার টেস্টের গাণিতিক সূত্র ব্যবহার করে এক্সেলে চ-স্কোয়ার পরীক্ষা করার সূত্রগুলি।

প্রকার

1. ফিটের সদ্ব্যবহারের জন্য চি-স্কোয়ার পরীক্ষা
2. দুটি ভেরিয়েবলের স্বাধীনতার জন্য চি-স্কয়ার পরীক্ষা

# 1 - ফিটের সার্থকতার জন্য চি-স্কোয়ার পরীক্ষা

এটি একটি জনসংখ্যার উপযোগী একটি নমুনার সান্নিধ্য বুঝতে ব্যবহৃত হয়। চি-স্কোয়ার পরীক্ষার প্রতীক (2)। এটি সকলের যোগফল (পর্যবেক্ষণ গণনা - প্রত্যাশিত গণনা 2 / প্রত্যাশিত গণনা।

• যেখানে k-1 ডিগ্রি স্বাধীনতা বা ডিএফ।
• কোথায় ওয় হয় পর্যবেক্ষণ ফ্রিকোয়েন্সি, কে বিভাগসমূহ, এবং ই আই প্রত্যাশিত ফ্রিকোয়েন্সি।

বিঃদ্রঃ:- একটি পরিসংখ্যানের মডেলের ফিটনেসের সদ্ব্যবহার্য নমুনা ডেটা পর্যবেক্ষণের একটি সেটকে কতটা ফিট করে তা বোঝার বোঝায়।

ব্যবহারসমূহ

• Ageণগ্রহীতাদের তাদের বয়স গ্রুপ এবং ব্যক্তিগত onণের উপর ভিত্তি করে worণযোগ্যতা
• বিক্রয়কর্মীদের কর্মক্ষমতা এবং প্রশিক্ষণের মধ্যকার সম্পর্ক
• একক স্টক এবং ফার্মাসিউটিক্যাল বা ব্যাংকিংয়ের মতো খাতের স্টকগুলিতে ফিরে আসুন
• দর্শকদের বিভাগ এবং একটি টিভি প্রচারের প্রভাব।

# 2 - দুটি ভেরিয়েবলের স্বাধীনতার জন্য চি-স্কয়ার পরীক্ষা

এটি ভেরিয়েবলগুলি একে অপরের স্বায়ত্তশাসিত কিনা তা পরীক্ষা করে ব্যবহার করা হয় ized (আর -1) (সি -1) স্বাধীনতার ডিগ্রি সহ

কোথায় ওয় হয় পর্যবেক্ষণ ফ্রিকোয়েন্সি, r সারি সংখ্যা, গ কলামের সংখ্যা এবং number ই আই প্রত্যাশিত ফ্রিকোয়েন্সি

বিঃদ্রঃ:- দুটি র্যান্ডম ভেরিয়েবলকে স্বাধীন বলা হয় যদি একটি ভেরিয়েবলের সম্ভাব্যতা বিতরণ অন্যটির দ্বারা প্রভাবিত না হয়।

ব্যবহারসমূহ

স্বাধীনতার পরীক্ষা নিম্নলিখিত পরিস্থিতিতে উপযুক্ত:

• একটি স্বতন্ত্র পরিবর্তনশীল আছে।
• দুটি শ্রেণীবদ্ধ ভেরিয়েবল রয়েছে এবং তাদের মধ্যে সম্পর্ক নির্ধারণ করতে আপনার প্রয়োজন হবে।
• ক্রস-ট্যাবুলেশনগুলি রয়েছে এবং দুটি শ্রেণিবদ্ধ ভেরিয়েবলের মধ্যে সম্পর্ক খুঁজে পাওয়া দরকার।
• অ-কোয়ান্টেফিয়েবল ভেরিয়েবলগুলি রয়েছে (উদাহরণস্বরূপ, প্রশ্নের উত্তরগুলির মতো, বিভিন্ন বয়সের কর্মচারীরা কি বিভিন্ন ধরণের স্বাস্থ্য পরিকল্পনা চয়ন করে?)

এক্সেলে চ-স্কয়ার টেস্টটি কীভাবে করবেন? (উদাহরণ সহ)

আপনি এই চি স্কোয়ার টেস্ট এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - চি স্কোয়ার টেস্ট এক্সেল টেম্পলেট

কোনও রেস্তোরাঁর ব্যবস্থাপক গ্রাহকের সন্তুষ্টি এবং টেবিলের জন্য অপেক্ষা করা লোকদের বেতনের মধ্যে সম্পর্ক খুঁজে পেতে চান। এটিতে, আমরা চি-স্কোয়ারটি পরীক্ষা করার জন্য অনুমান স্থাপন করব

• তিনি পরিষেবাটি দুর্দান্ত, ভাল বা দরিদ্র কিনা তা জিজ্ঞাসা করে 100 জন গ্রাহকের একটি এলোমেলো নমুনা নেন।
• তারপরে তিনি নিম্ন, মাঝারি এবং উচ্চতর হিসাবে অপেক্ষা করা ব্যক্তিদের বেতনগুলি শ্রেণিবদ্ধ করেন।
• ধরুন তাৎপর্যের স্তরটি 0.05 is এখানে, এইচ 0 এবং এইচ 1 টেবিলের অপেক্ষারত লোকদের বেতনের উপর পরিষেবার মানের স্বাধীনতা এবং নির্ভরতা বোঝায়।
• এইচ₀ - পরিষেবাগুলির মান টেবিলের জন্য অপেক্ষা করা লোকদের বেতনের উপর নির্ভর করে না।
• এইচ₁ - পরিষেবার মান টেবিলের জন্য অপেক্ষা করা লোকদের বেতনের উপর নির্ভরশীল
• তার অনুসন্ধানগুলি নীচে ছকে দেখানো হয়েছে:

এটিতে আমাদের কাছে 9 টি পয়েন্ট রয়েছে যার মধ্যে 3 টি গ্রুপ রয়েছে যার প্রত্যেকটি বেতনের বিষয়ে আলাদা বার্তা পেয়েছে এবং ফলাফলটি নীচে দেওয়া আছে।

এখন আমরা সমস্ত সারি এবং কলামগুলির যোগফল গণনা করতে চলেছি। আমরা সূত্রের সাহায্যে এটি করব, অর্থাৎ। সম। আমরা লিখেছি মোট কলামে মোট দুর্দান্ত = সুম (বি 4: ডি 4) এবং তারপরে এন্টার টিপুন।

এটা আমাদের দেবে 26। আমরা সমস্ত সারি এবং কলামগুলির সাথে একই সম্পাদন করব।

গণনা করতে স্বাধীনতা ডিগ্রি (ডিএফ) আমরা ব্যাবহার করি (আর -১) (সি -১)

ডিএফ = (3-1)(3-1)=2*2=4

• পরিষেবা বিভাগের 3 বিভাগ এবং বেতন 3 বিভাগে রয়েছে
• আমাদের মাঝারি বেতনের ২ 27 জন উত্তরদাতা (নীচে সারি, মাঝারি)
• আমাদের একটি ভাল পরিষেবা সহ সর্বশেষ ৫১ জন উত্তরদাতা রয়েছে (শেষ কলাম, মাঝামাঝি)

এখন আমাদের গণনা করতে হবে প্রত্যাশিত ফ্রিকোয়েন্সি: -

প্রত্যাশিত ফ্রিকোয়েন্সি সূত্র ব্যবহার করে গণনা করা যায়: -

• জন্য গণনা করা দুর্দান্ত আমরা মোট সংখ্যাটি ব্যবহার করব কম মোট সাথে দুর্দান্ত বিভক্ত এন দ্বারা

ধরুন আমাদের প্রথম সারি এবং 1 ম কলামের জন্য গণনা করতে হবে (= বি 7 * ই 4 / বি 9))। এটি ভোট গ্রাহকদের প্রত্যাশিত সংখ্যা দেবে দুর্দান্ত মানুষের বেতন হিসাবে পরিষেবা হিসাবে অপেক্ষা নিম্ন অর্থাত্ 8.32.

• ই₁₁₌­­(32*26)/100 = 8.32, ই₁₂ = 7.02, ই₁₃ = 10.66
• ই₂₁ = 16.32, ই₂₂ = 13.77, ই₂₃ = 20.91
• ই₃₁ = 7.36, ই₃₂ = 6.21, ই₃₃ = 9.41

একইভাবে সবার জন্য, আমাদের একই কাজ করতে হবে এবং সূত্রটি নীচের চিত্রটিতে প্রয়োগ করা হবে।

আমরা নীচে প্রদত্ত প্রত্যাশিত ফ্রিকোয়েন্সি টেবিলটি পেয়েছি: -

বিঃদ্রঃ:- ধরুন তাৎপর্যের স্তরটি 0.05 is এখানে, এইচ 0 এবং এইচ 1 টেবিলের অপেক্ষারত লোকদের বেতনের উপর পরিষেবার মানের স্বাধীনতা এবং নির্ভরতা বোঝায়।

প্রত্যাশিত ফ্রিকোয়েন্সি গণনার পরে আমরা একটি সূত্র ব্যবহার করে চি-স্কোয়ার ডেটা পয়েন্ট গণনা করব

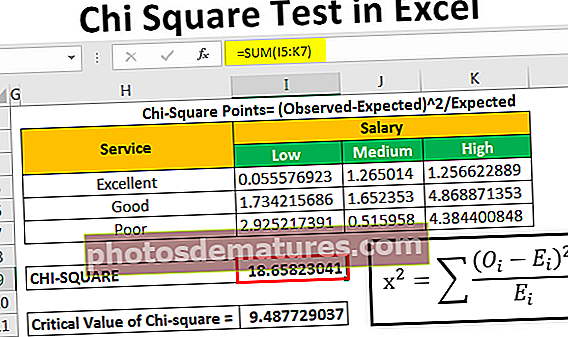
চি-স্কয়ার পয়েন্ট = (পর্যবেক্ষণ-প্রত্যাশিত) ^ 2 / প্রত্যাশিত

প্রথম পয়েন্টটি গণনা করার জন্য আমরা লিখি = (বি 4-বি 14) ^ 2 / বি 14।

আমরা স্বয়ংক্রিয়ভাবে মানটি পূরণ করতে অন্য কক্ষে সূত্রটি অনুলিপি করে কপি করব।

এর পরে, আমরা গণনা করব চি-মান (গণনা করা মান) টেবিলের উপরে দেওয়া সমস্ত মান যুক্ত করে

আমরা চি-মান হিসাবে পেয়েছি 18.65823.

এর জন্য সমালোচনামূলক মান গণনা করতে আমরা নীচে দেওয়া সূত্রটি ব্যবহার করতে পারি এর একটি চি-বর্গ সমালোচনামূলক মান সারণি ব্যবহার করি।

এই সূত্রে 2 টি পরামিতি রয়েছে CHISQ.INV.RT (সম্ভাবনা, স্বাধীনতার ডিগ্রি)।

সম্ভাবনা 0.05 হয়, এটি একটি উল্লেখযোগ্য মান যা আমাদের এটি গ্রহণ করতে হবে তা নির্ধারণ করতে সহায়তা করবে নাল হাইপোথেসিস (এইচ₀) অথবা না.

চি-স্কোয়ারের সমালোচনা মান 9.487729037.

এখন আমরা এর মান খুঁজে পাব চি-স্কোয়ার বা (পি মান)= CHITEST (আসল_আরঙ্গ, প্রত্যাশিত_আরঞ্জ)

পাল্লা হতে = CHITEST (বি 4: ডি 6, বি 14: ডি 16).

যেমনটি আমরা দেখেছি চি-টেস্ট বা পি-মানটির মান = 0.00091723।

যেমনটি আমরা দেখেছি যে আমরা সমস্ত মান গণনা করেছি। দ্য চি-বর্গ (গণনা করা মান) মানগুলি তখনই তাৎপর্যপূর্ণ হয় যখন এর মান একই বা তার চেয়ে বেশি হয় সমালোচনা মান 9.48, অর্থাত্ সমালোচনা মান (ট্যাবুলেটেড মান) এর চেয়ে বেশি হতে হবে 18.65 গ্রহণ করতে নাল হাইপোথেসিস (এইচ₀).

কিন্তু এখানে গণনা করা মান >সারণী মান

এক্স 2 (গণনা করা)> এক্স 2 (ট্যাবুলেটেড)

18.65>9.48

এই ক্ষেত্রে, আমরা এইটিকে প্রত্যাখ্যান করব নাল হাইপোথেসিস (এইচ₀) এবং বিকল্প (এইচ₁) গ্রহণ করা হবে।

• আমরা একই অর্থাত্ যদি ভবিষ্যদ্বাণী করতে পি-মানও ব্যবহার করতে পারি if পি-মান <= α (উল্লেখযোগ্য মান 0.05), নাল অনুমানকে প্রত্যাখ্যান করা হবে
• যদি পি-মান> α, করো না প্রত্যাখ্যান নাল অনুমান.

এখানে পি-মান (0.0009172)< α (0.05), এইচ প্রত্যাখ্যান করুন₀, এইচ গ্রহণ করুন₁

উপরের উদাহরণ থেকে, আমরা এই সিদ্ধান্তে পৌঁছেছি যে পরিষেবার মান অপেক্ষা করা লোকদের বেতনের উপর নির্ভরশীল।

মনে রাখার মতো ঘটনা

• একটি স্ট্যান্ডার্ড সাধারণ ভেরিয়েটের বর্গ হিসাবে বিবেচনা করে।
• বিভিন্ন ধারায় পর্যবেক্ষণ করা ফ্রিকোয়েন্সি নির্দিষ্ট অনুমানের সেটের অধীনে প্রত্যাশিত ফ্রিকোয়েন্সিগুলির তুলনায় উল্লেখযোগ্যভাবে পরিবর্তিত হয় কিনা তা মূল্যায়ন করে।
• একটি অনুমিত বিতরণ ডেটা ফিট করে তা নির্ধারণ করে।
• কন্টিনজেন্সি টেবিল ব্যবহার করে (বাজার গবেষণাগুলিতে, এই টেবিলগুলিকে ক্রস-ট্যাবগুলি বলা হয়)।
• নামমাত্র-স্তরের পরিমাপ সমর্থন করে।