এক্সেলের দীর্ঘমেয়াদী বিতরণ (সূত্র, উদাহরণ) | কিভাবে ব্যবহার করে?
পরিসংখ্যানগুলিতে আমাদের একটি লগনরমাল ডিস্ট্রিবিউশন নামে একটি শব্দ রয়েছে যা সাধারণত একটি ভেরিয়েবলের বিতরণ যাঁর লোগারিদম সাধারণত বিতরণ করা হয় তা খুঁজে বের করার জন্য গণনা করা হয়, মূল সূত্রটি এটি গণনা করার জন্য একটি খুব জটিল সূত্র তবে এক্সেলে আমাদের লগনরমাল গণনা করার জন্য একটি ইনবিল্ট ফাংশন রয়েছে বিতরণ যা Lognorm.Dist ফাংশন।
এক্সেলে লগনারমাল ডিস্ট্রিবিউশন কী
লগনারমাল বিতরণ একটি র্যান্ডম ভেরিয়েবলের একটি অবিচ্ছিন্ন পরিসংখ্যান বিতরণ প্রদান করে যা সাধারণত লোগারিদম বিতরণ করা হয়। নিম্নলিখিতটি এক্সলে ব্যবহৃত লগনিকাল ফাংশনগুলির প্রকার:
LOGNORM.DIST সূত্র
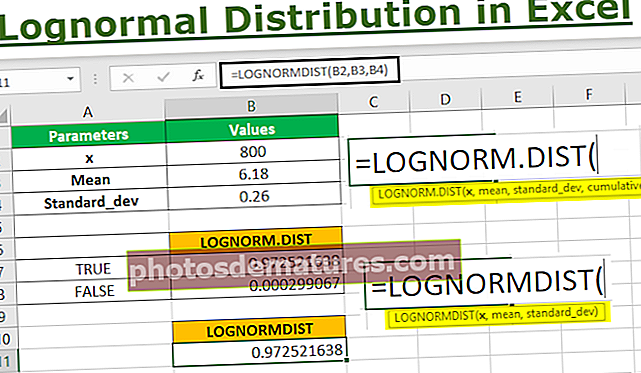
এক্সিলের বিতরণ ফাংশন সিনট্যাক্সকে LOGNORM.DIST (x, গড়, স্ট্যান্ডার্ড_দেব, ক্রমযুক্ত) হিসাবে সংজ্ঞায়িত করা হয় যা প্রাকৃতিক লোগারিদমের গড় এবং মানক বিচ্যুতির জন্য প্রদত্ত প্যারামিটার সহ এক্সের লগনরমাল বিতরণ প্রদান করে। উপরের ফাংশনটির জন্য নিম্নলিখিত পরামিতি বা আর্গুমেন্টগুলির প্রয়োজন: -

- x: - ‘x’ এর প্রয়োজনীয় মান যার লগনরমাল বিতরণটি ফেরত পাঠাতে হবে।
- গড়: - Ln (x) এর গড়
- মান_দেব: - Ln (x) এর মানক বিচ্যুতি
- সংশ্লেষক: - যদি संचयी সত্য হয় তবে ফাংশনটি संचयी বিতরণ ফিরিয়ে দেয়, অন্যথায় মিথ্যা সম্ভাবনার ঘনত্ব দেয়।
ক্রমবর্ধমান বিতরণ ফাংশন (সিডিএফ) একটি সম্ভাব্যতা পরিবর্তনশীল যা এক্স এর সমান থেকে কম মান নেয়। অবিচ্ছিন্ন র্যান্ডম ভেরিয়েবলের সম্ভাব্যতা ঘনত্ব ফাংশন (পিডিএফ) কোনও নির্দিষ্ট মান গ্রহণ করার জন্য এলোমেলো পরিবর্তনশীল x এর আপেক্ষিক সম্ভাবনা ব্যাখ্যা করে।
এছাড়াও LOGNORM.DIST সাধারণত শেয়ারের মূল্য বিশ্লেষণে কার্যকর কারণ স্টকগুলির মূল্য নির্ধারণের জন্য সাধারণ বিতরণ প্রয়োগ করা যায় না। ব্ল্যাক স্কোলস মডেলটির জন্য বিকল্প মূল্য গণনা করতেও এই ফাংশনটি ব্যবহার করা যেতে পারে।
লগনরমাল ডিস্ট্রিবিউশন এক্সেল পরামিতি গণনা করা হচ্ছে
আসুন আমরা এক্সেলে ব্যবহৃত লগমনরমাল বিতরণের জন্য কয়েকটি উদাহরণ দিয়ে যাই।
আপনি এই লগনারমাল ডিস্ট্রিবিউশন এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - লগনরমাল ডিস্ট্রিবিউশন এক্সেল টেম্পলেটগড় এবং স্ট্যান্ডার্ড বিচ্যুতি এক্সেল প্যারামিটারে পৌঁছানোর জন্য তালিকাবদ্ধ সংস্থাগুলির শেয়ার মূল্যের নীচে বিবেচনা করুন।

ধাপ 1:- এখন সম্পর্কিত স্টক মূল্যের জন্য প্রাকৃতিক লোগারিদম মান গণনা করুন।

উপরের তথ্য হিসাবে দেখা যাবে, = এলএন (সংখ্যা) প্রদত্ত সংখ্যার প্রাকৃতিক লোগারিদম মান প্রদান করে returns
ধাপ ২:- পরবর্তীটি প্রাকৃতিক লোগারিদম সংখ্যার স্কোয়ার মানগুলি গণনা করুন, এটি নীচের সারণীতে প্রদর্শিত হবে in

ধাপ 3:- স্ট্যান্ডার্ডের বিচ্যুতি গণনা করার জন্য এখন আমাদের স্টক মূল্যের প্রাকৃতিক লোগারিদমের যোগফল এবং স্কোয়ারড প্রাকৃতিক লোগারিদমের মানগুলির যোগফল প্রয়োজন।

পদক্ষেপ 4: - এর পরে স্টকের দামের জন্য প্রাকৃতিক লোগারিদমের গড়ের গণনা করুন।
গড়, µ = (5.97 + 5.99 + 6.21 + 6.54) / 4
বা µ = 6.18

পদক্ষেপ 5: স্ট্যান্ডার্ড বিচ্যুতির জন্য গণনাটি ম্যানুয়ালি এবং সরাসরি এক্সেল সূত্র ব্যবহার করে করা যেতে পারে।
নীচে স্টক দামের জন্য গড় এবং মান বিচ্যুতির মানগুলির জন্য সারণী রয়েছে is

স্ট্যান্ডার্ড বিচ্যুতিটি = এসটিডিইভি.এস (প্রাকৃতিক লোগারিদম কলামের রেঞ্জ (স্টকের মূল্য)) ব্যবহার করে গণনা করা হয়।
তবে, গড় এবং স্ট্যান্ডার্ড বিচ্যুতির জন্য উপরের প্যারামিটারগুলি কোনও প্রদত্ত মান ‘এক্স’, বা স্টক মূল্যের এক্সেল লগনরমাল বিতরণ গণনা করতে আরও ব্যবহার করা যেতে পারে। তার জন্য ব্যাখ্যা নীচে দেখানো হয়েছে।
ধাপ 1:- LOGNORM.DIST ফাংশন বুঝতে নীচের টেবিলটি বিবেচনা করুন

উপরের টেবিলটি এক্সের জন্য এক্সেল লগনারমাল বিতরণ গণনা করতে প্রয়োজনীয় প্যারামিটার মানগুলি দেখায়, যা 10 is
ধাপ ২:- এখন আমরা সূত্র ফাংশনে মানগুলি সন্নিবেশ করবো ফলাফলটিতে পৌঁছানোর জন্য, বি 2, বি 3, বি 4, এবং সংশ্লেষক পরামিতি নির্বাচন করার জন্য TRUE এবং FALSE বিকল্প থাকবে।
লগনার্ম.আইডিএসটি (এক্স, গড়, স্ট্যান্ডার্ড_দেব, ক্রমযুক্ত)

উপরের স্ক্রিনশটটিতে যেমন দেখানো হয়েছে তেমনি সংক্ষিপ্ত বিতরণ ক্রিয়াকলাপটি পেতে প্রথমে সত্য বিকল্পটি প্রবেশ করবে।

এর মাধ্যমে আমরা ক্রম বিতরণ ফাংশন (সিডিএফ) এর জন্য সেল সি 19 তে প্রদর্শিত মান অনুসারে পৌঁছেছি।
ধাপ 3:- এখন আসুন সংমিতি প্যারামিটারে একই যুক্তি B2, B3, B4 এবং FALSE নির্বাচন করে সম্ভাব্যতা ঘনত্ব ফাংশন (পিডিএফ) এর জন্য এক্সেলে লগনরমাল বিতরণ গণনা করা যাক।

উপরের চিত্রটিতে দেখা গেছে, আমরা সম্ভাব্য ঘনত্ব ফাংশন (পিডিএফ) এর জন্য সেল সি 20-এ ফলাফলটি পৌঁছেছি।
পদক্ষেপ 4: - উপরের ফাংশনে যেমন দেখা যায়, লোগোনআরএম.আইডিএসটি ২০১০ এক্সেলের সংস্করণ এবং তার পরে উপযুক্ত। তবে আমরা LOGNORMDIST ব্যবহার করতে পারি যা সর্বশেষতম সংস্করণগুলির মতো একই পরামিতি ব্যবহার করে। একই প্যারামিটারের মানগুলি বিবেচনা করে আমরা নীচে দেখানো অনুসারে LOGNORMDIST এর জন্য ফাংশনটি পপুলেট করব।

যেমন দেখা যায়, মানটি संचयी আর্গুমেন্টে সত্য পরামিতির জন্য LOGNORM.DIST হিসাবে একই চিত্রের ফলস্বরূপ।
এক্সেলে লগনরমাল বিতরণ সম্পর্কে মনে রাখার বিষয় Remember
- যদি কোনও প্যারামিটার বা যুক্তি অ-সংখ্যাসূচক হয় তবে লগনরমাল বিতরণ এক্সেলটি ফাংশনটি ফিরে আসবে # ভ্যালু! ভুল বার্তা.
- যদি আর্গুমেন্ট x এর চেয়ে কম এবং 0 এর সমান হয় বা যদি মান বিচ্যুতি 0 এর চেয়ে কম এবং সমান হয় তবে ফাংশনটি #NUM ফিরে আসবে! ভুল বার্তা.
- LOGNORM.DIST গণনা করার জন্য সমান অভিব্যক্তি হ'ল LOGNORM.DIST (x, গড়, মান_দেব) = NORM.S.DIST ((ln (x) -Man) / মান_দেব)
- এই ফাংশনটি ২০১০ এর সংস্করণ এবং পরবর্তী সংস্করণে সামঞ্জস্যপূর্ণ এবং 2007 এর আগের লোগোনারমডিআইএসটি (x, মানে, স্ট্যান্ডার্ড_দেব) ব্যবহার করা আবশ্যক, যা এক্সের সংশ্লেষিত লগমনরমাল বিতরণ ফিরিয়ে দেয়, যেখানে ln (x) সাধারণত প্যারামিটার / আর্গুমেন্টের সাথে বিতরণ করা হয় এবং মান_দেব।