photosdematures.com

অ্যাডজাস্টেড আর স্কোয়ার কী?

অ্যাডজাস্টেড আর স্কোয়ার্ডটি স্ট্যাটিস্টিকাল টুলকে বোঝায় যা বিনিয়োগকারীদের ভেরিয়েবলের প্রসারণের পরিমাণ পরিমাপ করতে সহায়তা করে যা নির্ভরশীল যা নির্ভরযোগ্য স্বাধীন ভেরিয়েবলের সাথে ব্যাখ্যা করা যেতে পারে এবং এটি কেবলমাত্র সেই স্বাধীন ভেরিয়েবলের প্রভাব বিবেচনা করে যার প্রকরণের উপর প্রভাব রয়েছে নির্ভরশীল পরিবর্তনশীল।

অ্যাডজাস্টেড আর স্কোয়ার্ড বা সংশোধিত আর ^ 2 নির্ভরশীল ভেরিয়েবলের তারতম্যের পরিমাণ নির্ধারণ করে যা স্বতন্ত্র ভেরিয়েবল দ্বারা ব্যাখ্যা করা যায়। পরিবর্তিত আর ^ 2 এর বৈশিষ্ট্যটি হ'ল এটি কেবল সমস্ত নির্ভরশীল ভেরিয়েবলের প্রভাবকে গণনা করে না যা নির্ভরশীল ভেরিয়েবলের প্রকরণকে প্রভাবিত করে। পরিবর্তিত আর ^ 2 এর মানটিও নেতিবাচক হতে পারে, যদিও এটি বেশিরভাগ সময় নেতিবাচক নয়।

সমন্বিত আর স্কোয়ারড ফর্মুলা

রিগ্রেশনের সমন্বিত আর স্কোয়ার গণনা করার সূত্রটি নীচে হিসাবে উপস্থাপিত হয়,

আর ^ 2 = {(1 / এন) * Σ [(এক্সআই - এক্স) * (ইয়ে - ই)] / (σx * σy) ^ ^ 2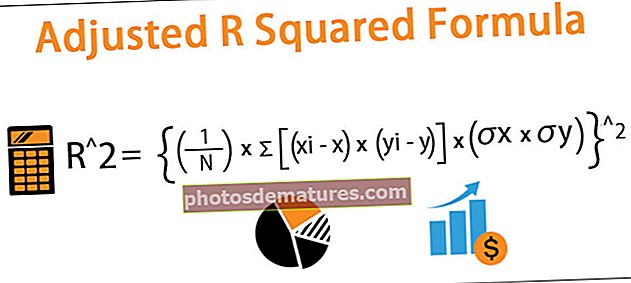

কোথায়

• আর ression 2 = রিগ্রেশন সমীকরণের সমন্বিত আর স্কোয়ার
• এন = রিগ্রেশন সমীকরণে পর্যবেক্ষণের সংখ্যা
• Xi = রিগ্রেশন সমীকরণের স্বতন্ত্র পরিবর্তনশীল
• এক্স = রিগ্রেশন সমীকরণের স্বাধীন ভেরিয়েবলের গড় Mean
• Yi = রিগ্রেশন সমীকরণের নির্ভরশীল পরিবর্তনশীল
• Y = রিগ্রেশন সমীকরণের নির্ভরশীল পরিবর্তনশীলের গড় Mean
• =x = স্বতন্ত্র ভেরিয়েবলের স্ট্যান্ডার্ড বিচ্যুতি
• =y = নির্ভরশীল ভেরিয়েবলের স্ট্যান্ডার্ড বিচ্যুতি।

দয়া করে নোট করুন

এক্সেলে এটি গণনা করার জন্য এটি এক্সেলে y এবং x ভেরিয়েবল সরবরাহ করা দরকার এবং এক্সেল দ্বারা অ্যাডজাস্টেড আর ^ 2 সহ পুরো আউটপুট উত্পন্ন হয়। এটি একটি বিশেষ ক্ষেত্রে যেখানে অন্য সূত্রের মতো পাঠ্য বিন্যাসে আউটপুট সরবরাহ করা কঠিন difficult

ব্যাখ্যা

অ্যাডজাস্টেড আর স্কোয়ার, নির্ভরশীল ভেরিয়েবলের বিস্তারের পরিমাণ নির্ধারণ করে যা স্বতন্ত্র ভেরিয়েবল দ্বারা ব্যাখ্যা করা যায়। অ্যাডজাস্টেড আর value 2 মানটি দেখে আপনি বিচার করতে পারেন যে রিগ্রেশন সমীকরণের ডেটাগুলি ভাল ফিট কিনা। অ্যাডজাস্টেড আর Higher 2 উচ্চতর রিগ্রেশন সমীকরণের উচ্চতর হিসাবে এটি সূচিত করে যে নির্ভরশীল ভেরিয়েবল নির্ধারণের জন্য স্বতন্ত্র পরিবর্তনশীলটি নির্ভরশীল ভেরিয়েবলের বিভিন্নতা ব্যাখ্যা করতে সক্ষম হয়।

পরিবর্তিত আর ^ 2 এর মানটিও নেতিবাচক হতে পারে, যদিও এটি বেশিরভাগ সময় নেতিবাচক নয়। অ্যাডজাস্টেড আর স্কোয়ারের ক্ষেত্রে, অ্যাডজাস্টেড আর স্কোয়ারের মানটি তখনই একটি স্বাধীন ভেরিয়েবলের সংযোজন সহ উঠে যাবে যখন স্বাধীন ভেরিয়েবলের প্রকরণটি নির্ভরশীল ভেরিয়েবলের প্রকরণকে প্রভাবিত করে। এটি আর ^ 2 এর ক্ষেত্রে প্রযোজ্য নয়, শুধুমাত্র অ্যাডজাস্টেড আর। 2 এর মানের ক্ষেত্রে প্রযোজ্য।

উদাহরণ

আপনি এই অ্যাডজাস্টেড আর স্কোয়ারড ফর্মুলা এক্সেল টেম্পলেটটি ডাউনলোড করতে পারেন - অ্যাডজাস্টেড আর স্কোয়ারড ফর্মুলা এক্সেল টেম্পলেট

উদাহরণ # 1

আসুন আমরা উদাহরণের সাহায্যে সমন্বিত আর। 2 এর ধারণাটি চেষ্টা করি এবং বুঝতে পারি। আসুন আমরা ট্রাক ড্রাইভারের দ্বারা আচ্ছাদিত দূরত্ব এবং ট্রাক ড্রাইভারের বয়সের মধ্যে কী সম্পর্ক রয়েছে তা জানার চেষ্টা করি। কেউ দুটি ভেরিয়েবলের মধ্যকার সম্পর্কের বিষয়ে যা ভাবেন, তা বৈধতা দেওয়ার জন্য আসলে রিগ্রেশন সমীকরণ করেন যা রিগ্রেশন সমীকরণের দ্বারাও বৈধ হয়।

এই বিশেষ উদাহরণে আমরা দেখতে পাব কোন পরিবর্তনশীল নির্ভরশীল পরিবর্তনশীল এবং কোন পরিবর্তনশীলটি স্বাধীন ভেরিয়েবল। এই রিগ্রেশন সমীকরণের নির্ভরশীল পরিবর্তনশীল হ'ল ট্রাক ড্রাইভারের দ্বারা আচ্ছাদিত দূরত্ব এবং স্বতন্ত্র ভেরিয়েবলটি ট্রাক চালকের বয়স। ভেরিয়েবলগুলির সাথে একটি রিগ্রেশন চালিয়ে আমরা অ্যাডজাস্টেড আর স্কোয়ার পেয়েছি 65%। নীচের স্ন্যাপশটটি ভেরিয়েবলগুলির জন্য রিগ্রেশন আউটপুট চিত্রিত করে। সংযুক্ত এক্সেল শীটে ডেটা সেট এবং ভেরিয়েবলগুলি উপস্থাপন করা হয়।

এই রিগ্রেশনটির 65% এর সমন্বিত আর ^ 2 মানটি ইঙ্গিত করে যে নির্ভরশীল ভেরিয়েবলের 65% তারতম্যটি স্বাধীন ভেরিয়েবল দ্বারা ব্যাখ্যা করা হয়। আদর্শভাবে, একজন গবেষক দৃ determination় সংকল্পের সহগের সন্ধান করবেন যা 100% এর নিকটতম।

উদাহরণ # 2

আসুন আমরা আর একটি উদাহরণের সাহায্যে সমন্বিত আর স্কোয়ারের ধারণাটি বোঝার চেষ্টা করি এবং বুঝতে পারি। আসুন আমরা একটি ক্লাসের শিক্ষার্থীদের উচ্চতা এবং সেই শিক্ষার্থীদের জিপিএ গ্রেডের মধ্যে কী সম্পর্ক তা জানার চেষ্টা করি। এই বিশেষ উদাহরণে আমরা দেখতে পাব কোন পরিবর্তনশীল নির্ভরশীল পরিবর্তনশীল এবং কোন পরিবর্তনশীলটি স্বাধীন ভেরিয়েবল। এই রিগ্রেশন সমীকরণের নির্ভরশীল পরিবর্তনশীল হ'ল শিক্ষার্থীদের জিপিএ এবং স্বতন্ত্র পরিবর্তনশীল শিক্ষার্থীদের উচ্চতা।

ভেরিয়েবলগুলির সাথে একটি রিগ্রেশন চালিয়ে আমরা সামঞ্জস্য করা R ^ 2 পেয়েছি नगনযোগ্য বা নেতিবাচক। নীচের স্ন্যাপশটটি ভেরিয়েবলগুলির জন্য রিগ্রেশন আউটপুট চিত্রিত করে। সংযুক্ত এক্সেল শীটে ডেটা সেট এবং ভেরিয়েবলগুলি উপস্থাপন করা হয়।

সমন্বিত আর ^ 2 মান এই রিগ্রেশনটির জন্য নগণ্য যা এর দ্বারা বোঝায় যে নির্ভরশীল ভেরিয়েবলের পার্থক্যটি স্বাধীন ভেরিয়েবল দ্বারা ব্যাখ্যা করা হয়নি। আদর্শভাবে, একজন গবেষক দৃ determination় সংকল্পের সহগের সন্ধান করবেন যা 100% এর নিকটতম।

ব্যাখ্যা

ডেটা সেটটি ভাল ফিট কিনা তা নির্ধারণের জন্য অ্যাডজাস্টেড আর স্কোয়ার একটি খুব গুরুত্বপূর্ণ আউটপুট। কেউ দুটি ভেরিয়েবলের মধ্যকার সম্পর্কের বিষয়ে যা ভাবেন, তাও বৈধতা সমীকরণের দ্বারা বৈধ হয় কিনা তা যাচাই করার জন্য কেউ আসলে রিগ্রেশন সমীকরণ করে। মান উচ্চতর, আরও ভাল রিগ্রেশন সমীকরণ যেমনটি সূচিত করে যে নির্ভরশীল ভেরিয়েবলটি সঠিকভাবে নির্ধারণের জন্য স্বতন্ত্র ভেরিয়েবলটি বেছে নেওয়া হয়। আদর্শভাবে, একজন গবেষক দৃ determination় সংকল্পের সহগের সন্ধান করবেন যা 100% এর নিকটতম।