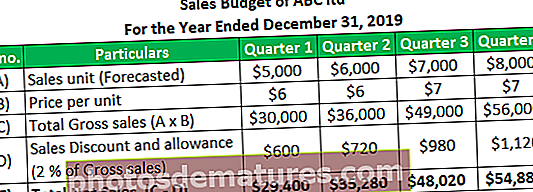
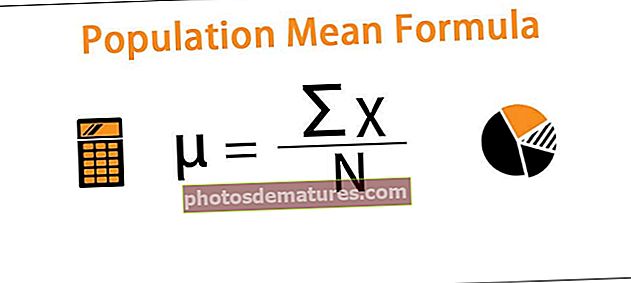জনসংখ্যা গড় সূত্র | জনসংখ্যা গড় গণনা (উদাহরণ)
জনসংখ্যা গড় গণনা করার সূত্র
জনসংখ্যার গড় প্রদত্ত জনসংখ্যার সমস্ত মানের গড় বা গড় এবং জনসংখ্যার মানগুলির সংখ্যার দ্বারা বিভক্ত X এর যোগফল দ্বারা সংখ্যায়িত সমস্ত মানের সমষ্টি দ্বারা গণনা করা হয় যা এন দ্বারা নির্দেশিত হয়।
এটি দলটির সমস্ত পর্যবেক্ষণ সংক্ষিপ্ত করে এবং পর্যবেক্ষণের সংখ্যার দ্বারা সংক্ষেপটি ভাগ করে এখানে পৌঁছেছে। যখন পরিসংখ্যানের পরামিতি গণনার জন্য ডেটার পুরো সেটটি নেওয়া হয়, তখন ডেটার সেটটি জনসংখ্যা। উদাহরণস্বরূপ ন্যাসডাক স্টক এক্সচেঞ্জের তালিকাভুক্ত সমস্ত স্টকের রিটার্ন group গ্রুপের জনসংখ্যায়। এই উদাহরণস্বরূপ, নাসডাক স্টক এক্সচেঞ্জে তালিকাভুক্ত সমস্ত স্টকের প্রত্যাবর্তনের জন্য জনসংখ্যা মানে সেই এক্সচেঞ্জের তালিকাভুক্ত সমস্ত স্টক ফিরতি গড় হবে।
জনগোষ্ঠী একটি গোষ্ঠীর জন্য গণনা করার জন্য আমাদের প্রথমে সমস্ত পর্যবেক্ষণকৃত মানগুলির যোগফল বের করতে হবে। সুতরাং, যদি পর্যবেক্ষণকৃত মানগুলির সংখ্যাটি X দ্বারা চিহ্নিত করা হয় তবে সমস্ত পর্যবেক্ষণকৃত মানগুলির সংমিশ্রণ হবে beX। এবং জনসংখ্যার পর্যবেক্ষণের সংখ্যাটি এন।
সূত্রটি নীচে উপস্থাপিত হয়,
µ = এক্স / এন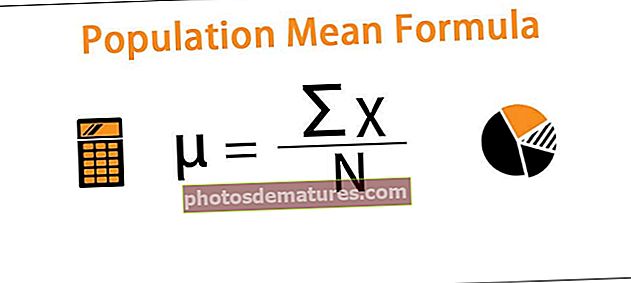
- µ = জনসংখ্যা মানে
উদাহরণ
আপনি এই জনসংখ্যা গড় সূত্র এক্সেল টেম্পলেটটি ডাউনলোড করতে পারেন - জনসংখ্যা গড় সূত্র এক্সেল টেম্পলেটউদাহরণ # 1
আসুন আমরা গত বারো বছর ধরে স্টক এক্সওয়াইজেডের রিটার্ন বিশ্লেষণ করার চেষ্টা করি। এবং গত বারো বছরে শেয়ারটির জন্য রিটার্নগুলি হল 12%, 25%, 16%, 14%, 40%, 15%, 13%, 17%, 23%, 13%, 17%, এবং 19%। পুরো জনসংখ্যার গড় গণনা করতে, আমাদের প্রথমে সমস্ত পর্যবেক্ষণকৃত মানগুলির সংমিশ্রণটি খুঁজে বের করতে হবে। সুতরাং এই উদাহরণে, ∑X হল 224% এবং জনসংখ্যার জন্য পর্যবেক্ষিত মানগুলির সংখ্যা 12 কারণ এটি 12 বছরের জন্য স্টকের জন্য ফেরত অন্তর্ভুক্ত করে।
এই দুটি ভেরিয়েবলের সাহায্যে আমরা সূত্রের সাহায্যে স্টক ফেরতের জন্য জনসংখ্যার গড় গণনা করতে পারি।
প্রদত্ত তথ্য নীচে দেওয়া হল

অতএব, উপরের তথ্যটি ব্যবহার করে গণনা করা যেতে পারে,

- µ = 224% / 12

উদাহরণটি দেখায় যে পর্যবেক্ষণকৃত মানটির গড় বা গড় আয় 19%।
উদাহরণ # 2
আসুন আমরা গত আট বছর ধরে থিম্যাটিক মিউচুয়াল ফান্ডের রিটার্ন বিশ্লেষণ করার চেষ্টা করি। এবং গত বারো বছরে শেয়ারটির রিটার্নগুলি 25%, 16%, 14%, 15%, 13%, 23%, 33%, এবং 27%% পুরো জনসংখ্যার গড় গণনা করতে, আমাদের প্রথমে সমস্ত পর্যবেক্ষণকৃত মানগুলির সংমিশ্রণটি খুঁজে বের করতে হবে। সুতরাং এই উদাহরণে, ∑X হল 166% এবং জনসংখ্যার জন্য পর্যবেক্ষণকৃত মানগুলির সংখ্যা 8 কারণ এটি 8 বছরের জন্য মিউচুয়াল ফান্ডের ফেরতকে অন্তর্ভুক্ত করে।
এই দুটি ভেরিয়েবলের সাহায্যে আমরা সূত্রের সাহায্যে স্টক ফেরতের জন্য জনসংখ্যার গড় গণনা করতে পারি।
নীচে গণনার জন্য ডেটা দেওয়া আছে

সুতরাং, গড় হিসাবে গণনা করা যেতে পারে,

- µ = 166% / 8

উদাহরণটি দেখায় যে পর্যবেক্ষণকৃত মানটির গড় বা গড় আয় 21%।
উদাহরণ # 3
আসুন জনগণের ক্লাসে 15 জন শিক্ষার্থীর ওজনের গড় খুঁজে বের করি। 15 কেজি প্রতি শিক্ষার্থীর ক্লাসের প্রতিটি শিক্ষার্থীর ওজন নিম্নরূপ 35, 36, 42, 40, 44, 45, 38, 42, 39, 42, 44, 45, 48, 42, এবং 40 হিসাবে রয়েছে পুরো জনসংখ্যার গড় গণনা করুন, আমাদের প্রথমে সমস্ত পর্যবেক্ষণকৃত মানগুলির সংমিশ্রণটি খুঁজে বের করতে হবে। সুতরাং এই উদাহরণে, ∑X 622 কেজি এবং জনসংখ্যার জন্য পর্যবেক্ষণকৃত মানগুলির সংখ্যা 15 কারণ এটি 15 শিক্ষার্থীর ওজনকে অন্তর্ভুক্ত করে।
এই দুটি ভেরিয়েবলের সাহায্যে আমরা সূত্রের সাহায্যে স্টক ফেরতের জন্য জনসংখ্যার গড় গণনা করতে পারি।
গণনার জন্য প্রদত্ত ডেটা নীচে দেওয়া হল

সুতরাং, উপরোক্ত তথ্য ব্যবহার করে জনসংখ্যার গড় হিসাবে গণনা করা যেতে পারে,

- µ = 622/15

উদাহরণটি দেখায় যে পর্যবেক্ষণকৃত মানটির গড় বা গড় প্রত্যাবর্তন 41.47
প্রাসঙ্গিকতা এবং ব্যবহার
জনসংখ্যা মানে একটি খুব গুরুত্বপূর্ণ পরিসংখ্যান পরামিতি। এটি জনসংখ্যার পরামিতিগুলির গড় জানতে সহায়তা করে। গড়টি গুরুত্বপূর্ণ কারণ এটি বিভিন্ন অন্যান্য পরিসংখ্যানগত পরামিতি যেমন বৈকল্পিক, মানক বিচ্যুতি এবং অন্যান্যগুলির গণনায় ব্যবহৃত হয়। এটি পাটিগণিত গড় সূত্রের ধারণাটি ব্যবহার করে গণনা করা হয় এবং গড় বা গড়কে উপস্থাপন করে যার ভিত্তিতে পর্যবেক্ষণের পুরো জনসংখ্যায় কোনও পর্যবেক্ষণ উচ্চ বা কম হয় কিনা তার উপর ভিত্তি করে কেউ একটি সূচনা করতে পারে।