photosdematures.com

পিয়ারসন সহসম্পর্ক সহগ সংজ্ঞা

পিয়ারসন পারস্পরিক সম্পর্ক সহগ, যা পিয়ারসন আর স্ট্যাটিস্টিকাল টেস্ট নামেও পরিচিত, বিভিন্ন ভেরিয়েবল এবং তাদের সম্পর্কের মধ্যে শক্তি পরিমাপ করে। যখনই কোনও পরিসংখ্যান পরীক্ষা দুটি ভেরিয়েবলের মধ্যে পরিচালিত হয়, তখন বিশ্লেষণ করা ব্যক্তির পক্ষে দুটি ভেরিয়েবলের মধ্যে সম্পর্ক কতটা দৃ strong় তা জানার জন্য পারস্পরিক সম্পর্কের সহগের মান গণনা করা সর্বদা একটি ভাল ধারণা।

পিয়ারসনের পারস্পরিক সম্পর্ক সহগ -1 এবং 1 এর মধ্যে একটি মান প্রদান করে the

• পারস্পরিক সম্পর্ক সহগ -1 হয়, এটি একটি দৃ a় নেতিবাচক সম্পর্ক নির্দেশ করে। এটি ভেরিয়েবলগুলির মধ্যে একটি নিখুঁত নেতিবাচক সম্পর্ক বোঝায়।
• পারস্পরিক সম্পর্ক সহগ 0 হলে এটি কোনও সম্পর্ক নির্দেশ করে না।
• পারস্পরিক সম্পর্ক সহগ 1 হলে এটি দৃ it় ইতিবাচক সম্পর্কের ইঙ্গিত দেয়। এটি ভেরিয়েবলগুলির মধ্যে একটি নিখুঁত ইতিবাচক সম্পর্ককে বোঝায়।

সম্পর্কের সহগের একটি উচ্চতর পরম মান ভেরিয়েবলের মধ্যে আরও দৃ a় সম্পর্ক নির্দেশ করে। সুতরাং, ০.7878 এর একটি সম্পর্কযুক্ত সহগটি 0.36 বলার মানের তুলনায় একটি শক্তিশালী ইতিবাচক পারস্পরিক সম্পর্ক নির্দেশ করে। একইভাবে, -0.40 বলার সাথে সম্পর্কযুক্ত সহগের তুলনায় -0.87 এর একটি সংযোগ সহগ একটি শক্তিশালী নেতিবাচক সম্পর্ককে নির্দেশ করে।

অন্য কথায়, মানটি যদি ধনাত্মক পরিসরে থাকে তবে এটি দেখায় যে ভেরিয়েবলের মধ্যে সম্পর্ক ইতিবাচকভাবে সম্পর্কিত হয় এবং উভয় মান হ্রাস বা একসাথে বৃদ্ধি পায়। অন্যদিকে, মানটি যদি negativeণাত্মক সীমার মধ্যে থাকে, তবে এটি দেখায় যে ভেরিয়েবলের মধ্যে সম্পর্কটি নেতিবাচকভাবে সম্পর্কিত হয়, এবং উভয় মানই বিপরীত দিকে চলে যাবে।

পিয়ারসন সহসাধন সহগের সূত্র

পিয়ারসন এর সম্পর্কযুক্ত সহগ সূত্রটি নিম্নরূপ,

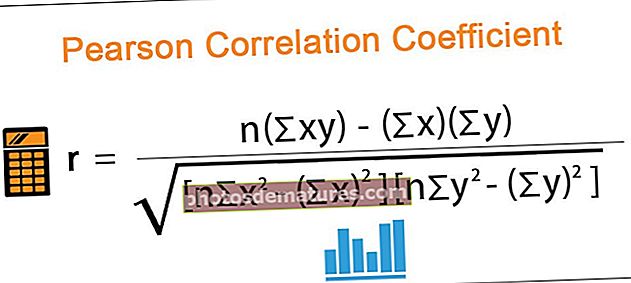
কোথায়,

• r = পিয়ারসন সহগ
• n = স্টকের জোড়গুলির সংখ্যা
• ∑xy = জোড়াযুক্ত স্টকের পণ্যের যোগফল
• X স্কোরের যোগফল = যোগফল
• =y = y স্কোরগুলির যোগফল
• 2x2 = স্কোয়ারড এক্স স্কোরগুলির যোগফল
• 2y2 = বর্গক্ষেত্রের y স্কোরগুলির যোগফল

ব্যাখ্যা

ধাপ 1: ভেরিয়েবলের জোড়া সংখ্যার সন্ধান করুন, যা এন দ্বারা চিহ্নিত করা হয়। আসুন ধরে নেওয়া যাক x 3 টি ভেরিয়েবলগুলি নিয়ে গঠিত - 6, 8, 10। আসুন আমরা ধরে নিই যে y 12, 10, 20 এর সাথে 3 টি ভেরিয়েবল নিয়ে গঠিত।

ধাপ ২: দুটি কলামে ভেরিয়েবল তালিকাভুক্ত করুন।

ধাপ 3: তৃতীয় কলামে x এবং y এর পণ্যটি সন্ধান করুন।

পদক্ষেপ 4: সমস্ত এক্স ভেরিয়েবল এবং সমস্ত y ভেরিয়েবলের মানগুলির যোগফল সন্ধান করুন। 1 ম এবং 2 য় কলামের নীচে ফলাফল লিখুন। তৃতীয় কলামে x * y এর যোগফল লিখুন।

পদক্ষেপ 5: চতুর্থ এবং 5 ম কলামে x2 এবং y2 এবং কলামগুলির নীচে তাদের যোগফল সন্ধান করুন।

পদক্ষেপ:: সূত্রটিতে উপরে পাওয়া মানগুলি সন্নিবেশ করান এবং এটি সমাধান করুন।

আর = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)

= 0.7559

পিয়ারসন সহসম্পর্ক সহগের উদাহরণ

আপনি এই পিয়ারসন কারেলিলেশন কোফিলিটি এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - পিয়ারসন সহসম্পর্কতা সহগ এক্সেল টেম্পলেট

উদাহরণ 1

এই উদাহরণে পিয়ারসন আর এর মূল্য গণনার জন্য নীচে প্রদত্ত পৃথক বয়স এবং বিভিন্ন ওজনযুক্ত 6 জনের সারণিতে নিম্নলিখিত বিবরণগুলির সাহায্যে

সমাধান:

পিয়ারসন সহকারী সহগের গণনার জন্য, আমরা প্রথমে নিম্নলিখিত মানগুলি গণনা করব,

এখানে মোট লোকের সংখ্যা 6 তাই, n = 6

এখন পিয়ারসন আর এর গণনা নিম্নরূপ:

• r = (n (∑xy) - (∑x) (∑y)) / (√ [n ∑x2- ()x) 2]] [n ∑y2– ()y) 2)
• আর = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• আর = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• আর = (83622- 82618) / (√ [43680 -40804] * [170190- 167281)
• আর = 1004 / (√ [2876] * [2909)
• আর = 1004 / (√ 8366284)
• আর = 1004 / 2892.452938
• r = 0.35

সুতরাং পিয়ারসন পারস্পরিক সম্পর্ক সহগের মান 0.35

উদাহরণ # 2

2 টি স্টক রয়েছে - এ এবং বি নির্দিষ্ট দিনগুলিতে তাদের শেয়ারের দাম নীচে রয়েছে:

উপরের তথ্য থেকে পিয়ারসন পারস্পরিক সম্পর্ক সহগ খুঁজে বের করুন।

সমাধান:

প্রথমত, আমরা নিম্নলিখিত মানগুলি গণনা করব।

পিয়ারসন সহগের গণনা নিম্নরূপ,

• r = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
• = -0.9088

সুতরাং দুটি স্টকের মধ্যে পিয়ারসন পারস্পরিক সম্পর্ক সহগ হয় -0.9088।

সুবিধাদি

• এটি দুটি ভেরিয়েবলের মধ্যে সম্পর্ক কতটা দৃ knowing় তা জানার ক্ষেত্রে সহায়তা করে। দুটি ভেরিয়েবলের মধ্যে পারস্পরিক সম্পর্কের উপস্থিতি বা অনুপস্থিতিই কেবল পিয়ারসন কারেলিলেশন কোফিলিটি ব্যবহার করে নির্দেশিত হয় না তবে এটি সঠিকভাবে নির্ধারণ করে যে এই ভেরিয়েবলগুলি সম্পর্কযুক্ত কিনা।
• এই পদ্ধতিটি ব্যবহার করে, কেউ পারস্পরিক সম্পর্কের দিকটি সনাক্ত করতে পারে অর্থাৎ দুটি ভেরিয়েবলের মধ্যে পারস্পরিক সম্পর্ক নেতিবাচক বা ধনাত্মক কিনা।

অসুবিধা

• নির্ভরশীল ভেরিয়েবল এবং স্বতন্ত্র ভেরিয়েবলের মধ্যে পার্থক্য বলতে পিয়েরসন কারেলিলেশন কোফিলিটি আর পর্যাপ্ত নয় কারণ ভেরিয়েবলগুলির মধ্যে সহসংযোগের সহগ প্রতিসম হয়। উদাহরণস্বরূপ, যদি কোনও ব্যক্তি উচ্চ চাপ এবং রক্তচাপের মধ্যে পারস্পরিক সম্পর্ক জানার চেষ্টা করছেন, তবে কেউ পরস্পরের সম্পর্কের উচ্চ মান খুঁজে পেতে পারেন যা দেখায় যে উচ্চ চাপ চাপের কারণে রক্তচাপ তৈরি করে। এখন যদি ভেরিয়েবলটি চারদিকে পরিবর্তন করা হয় তবে ফলাফল, সেই ক্ষেত্রে, একই রকম হবে যা দেখায় যে চাপটি রক্তচাপের কারণে ঘটেছিল যা কোনও অর্থহীন নয়। সুতরাং, গবেষককে বিশ্লেষণ পরিচালনার জন্য যে ডেটা ব্যবহার করছেন তা সম্পর্কে সচেতন হওয়া উচিত।
• এই পদ্ধতিটি ব্যবহার করে কেউ রেখার opeাল সম্পর্কে তথ্য পেতে পারে না কারণ এটি কেবলমাত্র দুটি ভেরিয়েবলের মধ্যে কোনও সম্পর্ক বিদ্যমান কিনা তা উল্লেখ করে।
• সম্ভবত পিয়ারসন কারেলিলেশন কোফিলিটির বিশেষত সমজাতীয় তথ্যের ক্ষেত্রে ভুল ব্যাখ্যা করা যেতে পারে।
• গণনার অন্যান্য পদ্ধতির সাথে তুলনা করা হলে, এই পদ্ধতিটি ফলাফলগুলিতে পৌঁছাতে অনেক সময় নেয়।

গুরুত্বপূর্ণ পয়েন্ট

• মানগুলি +1 থেকে শুরু করে মান -1 পর্যন্ত হতে পারে, যেখানে +1 বিবেচিত ভেরিয়েবলের মধ্যে নিখুঁত ধনাত্মক সম্পর্ককে নির্দেশ করে, -1 ভেরিয়েবলগুলির মধ্যে নিখুঁত নেতিবাচক সম্পর্ক নির্দেশ করে, এবং 0 মান নির্দেশ করে যে কোনও সম্পর্ক নেই বিবেচিত ভেরিয়েবলের মধ্যে বিদ্যমান।
• এটি ভেরিয়েবলগুলির পরিমাপের এককের থেকে পৃথক। উদাহরণস্বরূপ, যদি একটি ভেরিয়েবলের পরিমাপের একক বছরগুলিতে হয় এবং দ্বিতীয় ভেরিয়েবলের পরিমাপের এককটি কিলোগ্রামে হয়, তবুও, এই সহগের মান পরিবর্তন হয় না।
• ভেরিয়েবলের মধ্যে পারস্পরিক সম্পর্কের সহগ প্রতিসম হয় যার অর্থ Y এবং X বা X এবং Y এর মধ্যে পারস্পরিক সম্পর্ক সহগের মান একই থাকবে।

উপসংহার

পিয়ারসন কারেলিলেশন কোএফিলিটি হ'ল পারস্পরিক সম্পর্ক সহগের প্রকার যা দুটি ভেরিয়েবলের মধ্যকার সম্পর্কের প্রতিনিধিত্ব করে যা একই বিরতি বা একই অনুপাত স্কেলে পরিমাপ করা হয়। এটি দুটি ক্রমাগত ভেরিয়েবলের মধ্যে সম্পর্কের শক্তি পরিমাপ করে।

এটি কেবলমাত্র দুটি ভেরিয়েবলের মধ্যে পারস্পরিক সম্পর্কের উপস্থিতি বা অনুপস্থিতিকেই নির্দেশ করে না তবে এটি নির্ভর করে যে এই ভেরিয়েবলগুলি কীভাবে সম্পর্কযুক্ত। এটি ভেরিয়েবলগুলি পরিমাপের এককের থেকে পৃথক যেখানে পারস্পরিক সম্পর্ক সহগের মান +1 থেকে মান -1 পর্যন্ত হতে পারে। তবে নির্ভরশীল ভেরিয়েবল এবং স্বতন্ত্র ভেরিয়েবলের মধ্যে পার্থক্য বলা যথেষ্ট নয় to