পরিসংখ্যানগুলিতে জেড টেস্ট সূত্র | ধাপে ধাপ গণনা (উদাহরণ)
পরিসংখ্যানগুলিতে জেড টেস্ট গণনা করার সূত্র
পরিসংখ্যানগুলিতে জেড টেস্টটি হাইপোথিসিস টেস্টকে বোঝায় যা মানক বিচ্যুতি উপলব্ধ এবং নমুনা বড় হলে ক্ষেত্রে দুটি নমুনা গণনা করা অর্থ আলাদা কিনা তা নির্ধারণ করতে ব্যবহৃত হয়।
জেড = (এক্স - μ) / ơ থেকে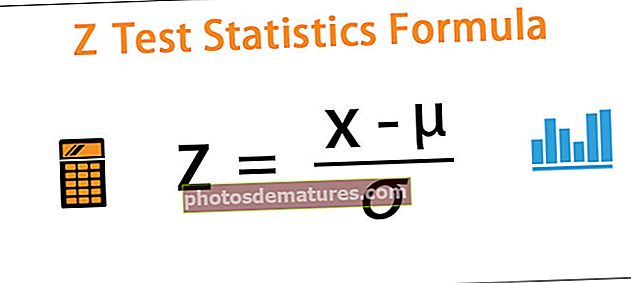
যেখানে x = জনসংখ্যার যে কোনও মান
- population = জনসংখ্যা গড়
- population = জনসংখ্যার মানক বিচ্যুতি
কোনও নমুনার ক্ষেত্রে, মানটির জেড-টেস্ট পরিসংখ্যানগুলির সূত্রটি x- মান থেকে নমুনা গড় কেটে গণনা করা হয় এবং তারপরে ফলাফলটি নমুনার স্ট্যান্ডার্ড বিচ্যুতি দ্বারা ভাগ করা হয়। গাণিতিকভাবে, এটি হিসাবে উপস্থাপিত হয়,
জেড = (এক্স - এক্স_মিয়ান)) / এসকোথায়
- এক্স = নমুনা থেকে কোনও মান
- x_mean = নমুনা গড়
- s = নমুনা স্ট্যান্ডার্ড বিচ্যুতি
জেড টেস্টের গণনা (ধাপে ধাপ)
জনসংখ্যার জেড-টেস্টের পরিসংখ্যানগুলির সূত্রটি নিম্নলিখিত পদক্ষেপগুলি ব্যবহার করে উত্পন্ন হয়েছে:
- ধাপ 1: প্রথমত, জনসংখ্যার অর্থ এবং জনসংখ্যায় ধরা পড়া পর্যবেক্ষণের ভিত্তিতে জনসংখ্যার মানক বিচ্যুতি গণনা করুন এবং প্রতিটি পর্যবেক্ষণ এক্স দ্বারা চিহ্নিত করা হয়েছেi। জনসংখ্যার মোট পর্যবেক্ষণের সংখ্যা এন দ্বারা চিহ্নিত করা হয়েছে
জনসংখ্যা মানে,

জনসংখ্যা স্ট্যান্ডার্ড বিচ্যুতি,

- ধাপ ২: পরিশেষে, জেড-টেস্টের পরিসংখ্যানগুলি ভেরিয়েবল থেকে জনসংখ্যার পরিমাণ হ্রাস করে গণনা করা হয় এবং তারপরে ফলাফলটি জনসংখ্যার মান বিচ্যুতি দ্বারা নীচে দেখানো হিসাবে ভাগ করা হয়।
জেড = (এক্স - μ) / ơ থেকে
একটি নমুনার জন্য জেড-পরীক্ষা পরিসংখ্যানের সূত্রটি নিম্নলিখিত পদক্ষেপগুলি ব্যবহার করে উত্পন্ন হয়েছে:
- ধাপ 1: প্রথমত, নমুনার গড় এবং নমুনার মান বিচ্যুতি উপরের মত গণনা করুন। এখানে, নমুনায় মোট পর্যবেক্ষণের সংখ্যা এন যেমন এন <এন দ্বারা চিহ্নিত করা হয়েছে।
নমুনা গড়,

নমুনা স্ট্যান্ডার্ড বিচ্যুতি,

- ধাপ ২: পরিশেষে, জেড-টেস্টের পরিসংখ্যানগুলি এক্স-মান থেকে নমুনা গড়কে বাদ দিয়ে গণনা করা হয় এবং তারপরে ফলাফলটি নীচের চিত্রের মতো নমুনা স্ট্যান্ডার্ড বিচ্যুতি দ্বারা ভাগ করা হয়।
জেড = (এক্স - এক্স_মিয়ান)) / এস
উদাহরণ
আপনি এই জেড টেস্ট সূত্র এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - জেড টেস্ট সূত্র এক্সেল টেম্পলেটউদাহরণ # 1
আসুন আমরা বিদ্যালয়ে এমন একটি জনসংখ্যার ছাত্রকে ধরে নিই যারা ক্লাস পরীক্ষায় অংশ নিয়েছিল। পরীক্ষার গড় স্কোর 75 এবং স্ট্যান্ডার্ড বিচ্যুতি 15. ডেভিডের জেড-টেস্টের স্কোর নির্ধারণ করুন যিনি টেস্টে 90 রান করেছিলেন।
দেওয়া,
- জনসংখ্যা মানে, μ = 75
- জনসংখ্যার মান বিচ্যুতি, ơ = 15

অতএব, z- পরীক্ষার পরিসংখ্যান হিসাবে গণনা করা যেতে পারে,

জেড = (90 - 75) / 15
জেড টেস্টের পরিসংখ্যানগুলি হ'ল -

- জেড = 1
সুতরাং, ডেভিডের পরীক্ষার স্কোর হ'ল জনসংখ্যার গড় স্কোরের তুলনায় একটি স্ট্যান্ডার্ড বিচ্যুতি, জেড-স্কোর টেবিল অনুসারে, শিক্ষার্থীদের ৮৪.১৩% ডেভিডের চেয়ে কম স্কোর।
উদাহরণ # 2
আসুন আমরা ৩০ জন শিক্ষার্থীর উদাহরণ নিই, যারা এক সপ্তাহে কতগুলি পেন্সিল ব্যবহার করা হচ্ছে তা দেখার জন্য সমীক্ষা করার জন্য একটি নমুনা দলের অংশ হিসাবে নির্বাচিত হয়েছিল। প্রদত্ত প্রতিক্রিয়াগুলির উপর ভিত্তি করে তৃতীয় শিক্ষার্থীর জেড-টেস্টের স্কোর নির্ধারণ করুন: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7।
দেওয়া,
- x = 5, তৃতীয় শিক্ষার্থীর প্রতিক্রিয়া হ'ল 5
- নমুনার আকার, এন = 30
নমুনাটির অর্থ, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30
গড় = 4.17
এখন, উপরের সূত্রটি ব্যবহার করে নমুনা স্ট্যান্ডার্ড বিচ্যুতি গণনা করা যেতে পারে।
ơ = 1.90
সুতরাং, তৃতীয় শিক্ষার্থীর জন্য জেড-পরীক্ষার স্কোর হিসাবে গণনা করা যেতে পারে,
জেড = (এক্স - এক্স) / সে
- জেড = (5 –17) / 1.90
- জেড = 0.44
সুতরাং, তৃতীয় শিক্ষার্থীর ব্যবহারের নমুনার গড় ব্যবহারের তুলনায় প্রমিত বিচ্যুতি 0.44 গুণ, অর্থাত্ জেড স্কোর সারণী অনুসারে, 67% শিক্ষার্থী তৃতীয় শিক্ষার্থীর চেয়ে কম পেন্সিল ব্যবহার করে।
উদাহরণ # 3
আসুন আমরা ৩০ জন শিক্ষার্থীর উদাহরণ নিই, যারা এক সপ্তাহে কতগুলি পেন্সিল ব্যবহার করা হচ্ছে তা দেখার জন্য সমীক্ষা করার জন্য একটি নমুনা দলের অংশ হিসাবে নির্বাচিত হয়েছিল। প্রদত্ত প্রতিক্রিয়াগুলির উপর ভিত্তি করে তৃতীয় শিক্ষার্থীর জেড-টেস্টের স্কোর নির্ধারণ করুন: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7।
নীচে জেড টেস্ট পরিসংখ্যান গণনার জন্য ডেটা দেওয়া হয়েছে


জেড টেস্ট পরিসংখ্যানের বিশদ গণনার জন্য আপনি নীচে প্রদত্ত এক্সেল শীটটি উল্লেখ করতে পারেন।
প্রাসঙ্গিকতা এবং ব্যবহার
জেড-টেস্টের পরিসংখ্যানের ধারণাটি বোঝার জন্য এটি খুব গুরুত্বপূর্ণ কারণ এটি পরীক্ষার পরিসংখ্যান সম্পর্কিত নাল অনুমানের অধীনে একটি সাধারণ বিতরণ অনুসরণ করে কিনা তা যখনই তর্কযোগ্য হয় তখনই এটি ব্যবহৃত হয়। যাইহোক, এটি মনে রাখা উচিত যে নমুনা আকার 30 এর চেয়ে বেশি হলেই জেড-পরীক্ষা ব্যবহার করা হয়, অন্যথায়, টি-পরীক্ষা ব্যবহার করা হয়।