পি মান সূত্র | পি-মান গণনা করার জন্য ধাপে ধাপে উদাহরণ
পি-মান সূত্র কী?
পি একটি পরিসংখ্যানগত পরিমাপ যা গবেষকদের তাদের অনুমানটি সঠিক কিনা তা নির্ধারণ করতে সহায়তা করে। এটি ফলাফলের তাৎপর্য নির্ধারণে সহায়তা করে। নাল অনুমানটি একটি ডিফল্ট অবস্থান যে দুটি পরিমাপের ঘটনার মধ্যে কোনও সম্পর্ক নেই। এটি এইচ দ্বারা চিহ্নিত করা হয়0. একটি বিকল্প অনুমানটি হ'ল আপনি যদি বিশ্বাস করেন যে নাল অনুমানটি অসত্য বলে প্রমাণিত হয়। এর প্রতীকটি এইচ1 বা এইচক।
এক্সেলে পি এর মান 0 এবং 1 এর মধ্যে একটি সংখ্যা is পি-মানটি গণনা করতে সহায়তার জন্য সারণী, স্প্রেডশিট প্রোগ্রাম এবং পরিসংখ্যান সংক্রান্ত সফ্টওয়্যার রয়েছে। তাত্পর্যপূর্ণ স্তর (α) গবেষক দ্বারা সেট করা একটি পূর্ব-সংজ্ঞায়িত প্রান্তিকতা। এটি সাধারণত 0.05 হয়। একটি খুব ছোট পি-মান, যা তাত্পর্যপূর্ণ স্তরের চেয়ে কম, এটি ইঙ্গিত করে যে আপনি নাল অনুমানটিকে প্রত্যাখ্যান করেন। পি-মান যা তাত্পর্য স্তরের চেয়ে বেশি তা নির্দেশ করে যে আমরা নাল অনুমানটিকে প্রত্যাখ্যান করতে ব্যর্থ।
পি-মান সূত্রের ব্যাখ্যা
পি-মান গণনার সূত্রটি নিম্নলিখিত পদক্ষেপগুলি ব্যবহার করে উত্পন্ন করা যেতে পারে:
একটি জেড স্ট্যাটিস্টিক থেকে পি-মান গণনা করা
ধাপ 1: আমাদের পরীক্ষার পরিসংখ্যান z জানতে হবে


কোথায়
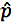 নমুনা অনুপাত হয়
নমুনা অনুপাত হয়- নল হাইপোথেসিসে পি 0 হ'ল জনসংখ্যা অনুপাত
- n হল নমুনা আকার
ধাপ ২: প্রাপ্ত z মান থেকে আমাদের পি স্তরের সংশ্লিষ্ট স্তরের সন্ধান করতে হবে। এই উদ্দেশ্যে, আমাদের z টেবিলটি দেখতে হবে।

উৎস: www.dummies.com
উদাহরণস্বরূপ, আসুন আমরা z ≥ 2.81 এর সাথে সম্পর্কিত পি এর মান সন্ধান করি। যেহেতু সাধারণ বিতরণ প্রতিসম হয় তাই z এর নেতিবাচক মানগুলি এর ধনাত্মক মানের সমান। 2.81 হল 2.80 এবং 0.01 এর যোগফল। জেড কলামে 2.8 দেখুন এবং এর সাথে সম্পর্কিত মান 0.01 value আমরা পি = 0.0025 পাই।
পি-মান সূত্রের উদাহরণ (এক্সেল টেম্পলেট সহ)
এর আরও ভাল করে বুঝতে পি-মান সমীকরণের কয়েকটি সহজ থেকে উন্নত উদাহরণগুলি দেখুন Let
আপনি এই পি মান সূত্র এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - পি মান সূত্র এক্সেল টেম্পলেট
উদাহরণ # 1
ক) পি-মান 0.3015। যদি তাৎপর্যের স্তরটি 5% হয়, তবে আমরা নাল অনুমানটি বাতিল করতে পারি কিনা তা সন্ধান করুন।
খ) পি-মান 0.0129। যদি তাৎপর্যের স্তরটি 5% হয়, তবে আমরা নাল অনুমানটি বাতিল করতে পারি কিনা তা সন্ধান করুন।
সমাধান:
পি-মান গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

পি-মান হবে -

ক) যেহেতু 0.3015 এর পি-মান 0.05 (5%) এর তাত্পর্যপূর্ণ স্তরের চেয়ে বেশি, তাই আমরা নাল অনুমানটিকে প্রত্যাখ্যান করতে ব্যর্থ হই।
খ) যেহেতু 0.0129 এর পি-মান 0.05 এর তাত্পর্যপূর্ণ স্তরের তুলনায় কম, তাই আমরা নাল অনুমানকে প্রত্যাখ্যান করি।
উদাহরণ # 2
একটি গবেষণা সমীক্ষা অনুসারে ভারতে ২ 27% মানুষ হিন্দি কথা বলে। একজন গবেষক তার গ্রামে এই সংখ্যাটি বেশি হলে আগ্রহী। সুতরাং, তিনি নাল এবং বিকল্প অনুমান ফ্রেম করেন। সে এইচ0: পি = 0.27। এইচএকটি: p> 0.27। এখানে, পি হিন্দি ভাষায় কথা বলার লোকদের অনুপাত। হিন্দি বলতে পারে এমন লোকের সংখ্যা জানতে তিনি তাঁর গ্রামে একটি সমীক্ষা চালিয়েছেন। তিনি দেখতে পান যে নমুনাযুক্ত 240 জনের মধ্যে 80 জন হিন্দি বলতে পারেন। গবেষকের পরীক্ষার জন্য আনুমানিক পি-মানটি সন্ধান করুন যদি আমরা ধরে নিই যে প্রয়োজনীয় শর্ত পূরণ হয়েছে এবং তাত্পর্য স্তর 5% is
সমাধান:
পি-মান গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

এখানে, নমুনার আকার n = 240,
পি0 জনসংখ্যার অনুপাত হ'ল আমাদের নমুনার অনুপাত খুঁজতে হবে 
= 80 / 240
 = 0.33
= 0.33
জেড স্ট্যাটিস্টিক
জেড স্ট্যাটিস্টিকের গণনা


=0.33 – 0.27 / √ 0.27 * (1 – 0.27 ) / 240
জেড পরিসংখ্যান হবে -

জেড = 2.093696
পি মান হবে -

পি মান = পি (z ≥ 2.09)
আমাদের দেখতে হবে 2.09 এর মানটি z টেবিল। সুতরাং, আমাদের z কলামে -2.0 এবং 0.09 কলামে মান দেখতে হবে। যেহেতু সাধারণ বিতরণ প্রতিসম হয়, তাই বক্ররেখার ডান দিকের অঞ্চলটি সমান is আমরা 0.0183 হিসাবে পি-মান পাই।
পি মান = 0.0183
যেহেতু পি-মানটি 0.05 (5%) এর তাত্পর্যপূর্ণ স্তরের চেয়ে কম, তাই আমরা নাল অনুমানকে প্রত্যাখ্যান করি।
বিঃদ্রঃ: এক্সেলে, পি-মানটি 0.0181 হিসাবে আসছে
উদাহরণ # 3
অধ্যয়নগুলি দেখায় যে মহিলাদের তুলনায় পুরুষরা বেশি সংখ্যক বিমানের টিকিট কিনেছেন। তারা 2: 1 এর অনুপাতে পুরুষ এবং মহিলা দ্বারা কিনেছেন। পুরুষ ও স্ত্রীদের মধ্যে বিমানের টিকিটের বিতরণ জানতে ভারতের একটি বিশেষ বিমানবন্দরে এই গবেষণা চালানো হয়েছিল। ১৫০ টি টিকিটের মধ্যে ৮৮ টি টিকিট পুরুষ কিনে এবং 62২ টি মহিলা কিনেছিলেন। পরীক্ষামূলকভাবে কারসাজির ফলে ফলাফলের পরিবর্তন ঘটে বা আমরা একটি সুযোগের তারতম্যটি পর্যবেক্ষণ করছি কিনা তা খুঁজে বের করতে হবে। তাত্পর্যটির ডিগ্রি 0.05 ধরে ধরে পি-মান গণনা করুন।
সমাধান:
পি-মান গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

ধাপ 1: পর্যবেক্ষণকৃত মানটি পুরুষদের জন্য 88 এবং মহিলাদের জন্য 62।
- পুরুষদের জন্য প্রত্যাশিত মান = 2/3 * 150 = 100 জন পুরুষ
- মহিলাদের জন্য প্রত্যাশিত মান = 1/3 * 150 = 50 মহিলা
ধাপ ২: চি-স্কোয়ার সন্ধান করুন


=((88-100)2)/100 + (62-50) 2/50
=1.44+2.88
চি-স্কোয়ার (এক্স ^ 2)
চি-স্কোয়ার (এক্স ^ 2) হবে -

চি-স্কোয়ার (এক্স ^ 2) = 4.32
ধাপ 3: স্বাধীনতার ডিগ্রি সন্ধান করুন
যেহেতু 2 টি ভেরিয়েবল রয়েছে - পুরুষ এবং মহিলা, n = 2
স্বাধীনতার ডিগ্রি = n-1 = 2-1 =
পদক্ষেপ 4: পি-মান সারণী থেকে, আমরা টেবিলে প্রথম সারির দিকে তাকিয়ে থাকি কারণ স্বাধীনতার ডিগ্রি ১.আমরা দেখতে পাচ্ছি যে পি-মান 0.025 এবং 0.05 এর মধ্যে রয়েছে। যেহেতু পি-মানটি 0.05 এর তাত্পর্যটির চেয়ে কম, তাই আমরা নাল অনুমানকে প্রত্যাখ্যান করি।
পি-মান হবে -

পি মান = 0.037666922
বিঃদ্রঃ: এক্সেল সরাসরি সূত্রটি ব্যবহার করে পি-মান দেয়:
CHITEST (আসল পরিসর, প্রত্যাশিত ব্যাপ্তি)
উদাহরণ # 4
এটি জানা যায় যে 60% লোক যারা কোনও শহরে পোশাকের দোকানগুলিতে প্রবেশ করে তারা কিছু কিনে ফেলে। একজন পোশাকের দোকানের মালিক তার মালিকানাধীন পোশাকের দোকানের জন্য সংখ্যাটি বেশি কিনা তা জানতে চেয়েছিলেন। তিনি ইতিমধ্যে তার দোকানের জন্য পরিচালিত একটি সমীক্ষার ফলাফল পেয়েছিলেন। তাঁর দোকানে প্রবেশ করা 200 জনের মধ্যে 128 জন কিছু কিনেছিলেন। দোকানের মালিক তার পোশাকের দোকানে প্রবেশ করে এবং কিছু কেনা লোকের অনুপাতের কথা উল্লেখ করেছেন। তাঁর দ্বারা নির্মিত নাল অনুমানটি ছিল p = 0.60 এবং বিকল্প অনুমানটি পি> 0.60 ছিল। 5% এর তাত্পর্যপূর্ণ স্তরে গবেষণার জন্য পি-মানটি সন্ধান করুন।
সমাধান:
পি-মান গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

এখানে, নমুনার আকার n = 200. আমাদের নমুনার অনুপাতটি খুঁজতে হবে
= 128 / 200
 = 0.64
= 0.64
জেড স্ট্যাটিস্টিক
জেড স্ট্যাটিস্টিকের গণনা


= 0.64 – 0.60 / √ 0.60 * (1 – 0.60) /200
জেড পরিসংখ্যান হবে -

জেড স্ট্যাটিস্টিক =1.1547
পি মান = পি (z ≥ 1.1547)
এক্সেলের মধ্যে NORMSDIST ফাংশন

NORMSDIST হবে -

উত্তর = 0.875893461
এক্সেলের একটি z পরিসংখ্যান থেকে একটি পি-মান গণনা করার জন্য একটি ইনবিল্ট ফাংশন রয়েছে। এটি NORMSDIST ফাংশন হিসাবে পরিচিত। এক্সেল NORMSDIST ফাংশন সরবরাহিত মান থেকে স্ট্যান্ডার্ড নরমাল ক্রমবর্ধমান বিতরণ ফাংশন গণনা করে। এর বিন্যাসটি NORMSDIST (z)। যেহেতু z পরিসংখ্যানের মানটি B2 ঘরে রয়েছে তাই ব্যবহৃত ফাংশনটি = NORMSDIST (B2)।
পি মান হবে -

পি মান = 0.12410654
যেহেতু আমাদের বক্ররেখার ডানদিকে অঞ্চলটি খুঁজতে হবে,
পি-মান = 1 - 0.875893 = 0.124107
যেহেতু 0.124107 এর পি-মান 0.05 এর একটি তাত্পর্যপূর্ণ স্তরের চেয়ে বেশি, তাই আমরা নাল অনুমানটিকে প্রত্যাখ্যান করতে ব্যর্থ।
প্রাসঙ্গিকতা এবং ব্যবহার
পি-মানটির পরিসংখ্যান অনুমানের পরীক্ষায় বিস্তৃত অ্যাপ্লিকেশন রয়েছে, বিশেষত নাল অনুমানের পরীক্ষায়। উদাহরণস্বরূপ, একটি তহবিল ব্যবস্থাপক একটি মিউচুয়াল ফান্ড পরিচালনা করে। তিনি দাবি করেছেন যে মিউচুয়াল ফান্ডের একটি বিশেষ স্কিম থেকে প্রাপ্ত রিটার্নগুলি নিফটির সমতুল্য, যা বেঞ্চমার্ক শেয়ার বাজার সূচক। তিনি নাল কল্পনাটি ফ্রেম করবেন যে মিউচুয়াল ফান্ড প্রকল্পের রিটার্নগুলি নিফটির সমান। বিকল্প অনুমানটি হ'ল স্কিমটির রিটার্ন এবং নিফটির রিটার্ন সমতুল্য নয়। তারপরে তিনি পি-মান গণনা করতেন।

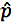 নমুনা অনুপাত হয়
নমুনা অনুপাত হয়