নমুনা ত্রুটির সূত্র | উদাহরণ সহ ধাপে ধাপ গণনা
নমুনা ত্রুটির গণনা করার সূত্র
স্যাম্পলিংয়ের ত্রুটির সূত্র পরিসংখ্যানগত ত্রুটি গণনা করার জন্য যে সূত্রটি ব্যবহৃত হয় সেটিকে বোঝায় যা পরীক্ষা পরিচালিত ব্যক্তি সেই নমুনা নির্বাচন করেন না যা বিবেচনাধীন পুরো জনগোষ্ঠীকে উপস্থাপন করে এবং সূত্র অনুসারে স্যাম্পলিং ত্রুটির মানক বিচ্যুতি বিভাজন করে গণনা করা হয় নমুনার আকারের বর্গমূল দ্বারা জনসংখ্যা এবং তারপরে জেড স্কোর মান দিয়ে ফলাফলকে গুণ করে যা আত্মবিশ্বাসের ব্যবধানের ভিত্তিতে থাকে।
নমুনা ত্রুটি = জেড এক্স (σ /√এন)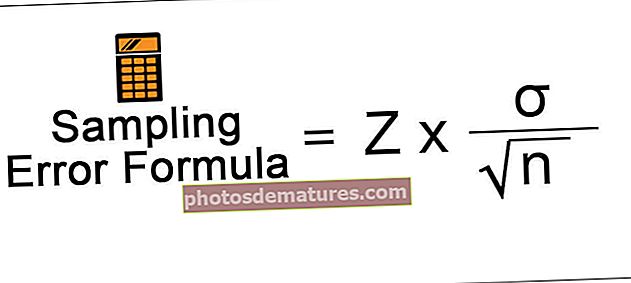
কোথায়,
- আত্মবিশ্বাসের ব্যবধানের ভিত্তিতে জেড হল জেড স্কোর মান
- σ হ'ল জনসংখ্যার মানক বিচ্যুতি
- n নমুনার আকার
নমুনা ত্রুটির ধাপে ধাপে গণনা
- ধাপ 1: জনসংখ্যা নামে পরিচিত সমস্ত ডেটা সংগ্রহ করে। জনসংখ্যার অর্থ এবং জনসংখ্যার মানক বিচ্যুতি গণনা করুন।
- ধাপ ২: এখন, নমুনার আকার নির্ধারণ করা দরকার এবং আরও নমুনার আকার জনসংখ্যার চেয়ে কম হওয়া উচিত এবং এটির চেয়ে বেশি হওয়া উচিত নয়।
- ধাপ 3: আত্মবিশ্বাসের স্তর নির্ধারণ করুন এবং তদনুযায়ী কেউ এর সারণী থেকে জেড স্কোরের মান নির্ধারণ করতে পারে।
- পদক্ষেপ 4: এখন জনসংখ্যার স্ট্যান্ডার্ড বিচ্যুতি দ্বারা জেড স্কোরকে গুণিত করুন এবং ত্রুটি বা নমুনা আকারের ত্রুটির প্রান্তরে পৌঁছানোর জন্য নমুনা আকারের বর্গমূলের সাথে একই ভাগ করুন।
উদাহরণ
আপনি এই নমুনা ত্রুটি সূত্র এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - স্যাম্পলিং ত্রুটির সূত্র এক্সেল টেম্পলেটউদাহরণ # 1
মনে করুন জনসংখ্যার মান বিচ্যুতি 0.30 এবং নমুনার আকার 100 হয়। 95% আস্থা স্তরে নমুনা ত্রুটিটি কী হবে?
সমাধান
এখানে আমাদের জনসংখ্যার মান বিচ্যুতি পাশাপাশি নমুনার আকার দেওয়া হয়, সুতরাং আমরা একই গণনা করতে নীচের সূত্রটি ব্যবহার করতে পারি।
গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, নমুনা ত্রুটির গণনা নিম্নরূপ,

নমুনা ত্রুটি হবে -

উদাহরণ # 2
গৌতম বর্তমানে একাউন্টেন্সি কোর্স করছে এবং সে তার প্রবেশিকা পরীক্ষা সাফ করেছে। তিনি এখন অন্তর্বর্তী স্তরের জন্য নিবন্ধন করেছেন এবং ইন্টার্ন হিসাবে সিনিয়র অ্যাকাউন্টেন্টে যোগ দেবেন। তিনি উত্পাদনকারী সংস্থাগুলির একটি নিরীক্ষণে কাজ করবেন।
তিনি যে ফার্মগুলির প্রথমবার পরিদর্শন করেছিলেন তার মধ্যে একটিতে, কেনার জন্য সমস্ত প্রবেশের বিল যুক্তিসঙ্গতভাবে পাওয়া যায় কিনা তা যাচাই করতে বলা হয়েছিল। নমুনার আকার তিনি বেছে নিয়েছিলেন 50 এবং এর জন্য জনসংখ্যার মান বিচ্যুতি 0.50 ছিল।
উপলভ্য তথ্যের ভিত্তিতে, আপনার নমুনা ত্রুটি 95% এবং 99% আত্মবিশ্বাসের ব্যবধানে গণনা করতে হবে।
সমাধান
এখানে আমাদের জনসংখ্যার মান বিচ্যুতি পাশাপাশি নমুনার আকার দেওয়া হয়, সুতরাং আমরা একই গণনা করতে নীচের সূত্রটি ব্যবহার করতে পারি।
95% আত্মবিশ্বাসের স্তরের জেড স্কোরটি হবে 1.96 (জেড স্কোর টেবিল থেকে উপলব্ধ)
গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, গণনাটি নিম্নরূপ:

নমুনা ত্রুটি হবে -

95% আত্মবিশ্বাসের স্তরের জেড স্কোর 2.58 হবে (জেড স্কোর টেবিল থেকে উপলব্ধ)
গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, গণনাটি নিম্নরূপ:

নমুনা ত্রুটি হবে -

আত্মবিশ্বাসের স্তর বাড়ার সাথে সাথে নমুনার ত্রুটিও বৃদ্ধি পায়।
উদাহরণ # 3
একটি স্কুলে, বায়োমেট্রিক অধিবেশনটি যাতে শিক্ষার্থীদের স্বাস্থ্য পরীক্ষা করতে হয় তার ব্যবস্থা করা হয়েছিল। দশম শ্রেণির শিক্ষার্থীদের নিয়ে এই অধিবেশনটির সূচনা হয়েছিল। বি বিভাগে মোট ৩০ জন শিক্ষার্থী রয়েছেন। তাদের মধ্যে 12 জন শিক্ষার্থীকে এলোমেলোভাবে বিশদ চেকআপ করতে বাছাই করা হয়েছিল এবং বাকি ছিল, কেবলমাত্র একটি বেসিক পরীক্ষা করা হয়েছিল। রিপোর্টটি অনুমান করা হয়েছে যে বি বিভাগে শিক্ষার্থীদের গড় উচ্চতা 154।

সমাধান
জনসংখ্যার মান বিচ্যুতি ছিল 9.39। উপরের তথ্যের উপর ভিত্তি করে, আপনাকে 90% এবং 95% আত্মবিশ্বাসের ব্যবধানের জন্য স্যাম্পলিং ত্রুটি গণনা করতে হবে।
এখানে আমাদের জনসংখ্যার স্ট্যান্ডার্ড বিচ্যুতি পাশাপাশি নমুনার আকার দেওয়া হয়, সুতরাং আমরা একই গণনা করতে নীচের সূত্রটি ব্যবহার করতে পারি।
95% আত্মবিশ্বাসের স্তরের জেড স্কোরটি হবে 1.96 (জেড স্কোর টেবিল থেকে উপলব্ধ)
গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, নমুনা ত্রুটির গণনা নিম্নরূপ,

নমুনা ত্রুটি হবে -

90% আত্মবিশ্বাসের স্তরের জেড স্কোরটি হবে 1.645 (জেড স্কোর টেবিল থেকে উপলব্ধ)
গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, গণনাটি নিম্নরূপ:

নমুনা ত্রুটি হবে -

আত্মবিশ্বাসের মাত্রা হ্রাস পাওয়ার সাথে সাথে নমুনার ত্রুটিও হ্রাস পায়।
প্রাসঙ্গিকতা এবং ব্যবহার
এটি এই ধারণাটি বোঝার পক্ষে অত্যন্ত গুরুত্বপূর্ণ কারণ এটি জরিপের ফলাফলগুলি বাস্তবে সামগ্রিকভাবে জনগণের প্রকৃত দৃষ্টিভঙ্গিকে চিত্রিত করবে এমন প্রত্যাশা কতটা করতে পারে তা চিত্রিত করে। একজনকে একটি বিষয় মনে রাখতে হবে যে একটি বৃহত জনসংখ্যার প্রতিনিধিত্ব করার জন্য একটি সমীক্ষাটি নমুনা আকার (অন্যথায় জরিপের প্রতিক্রিয়াকারী হিসাবে খ্যাত) নামে একটি ছোট জনসংখ্যার ব্যবহার করেও করা হয়।
এটি জরিপের কার্যকারিতা গণনা করার একটি উপায় হিসাবে দেখা যেতে পারে। স্যাম্পলিংয়ের মার্জিন বেশি হলে এটি উপস্থাপন করবে যে সমীক্ষার ফলাফলগুলি প্রকৃত মোট জনসংখ্যার প্রতিনিধিত্ব থেকে বিপথগামী হতে পারে। ফ্লিপ দিকে, একটি নমুনা ত্রুটি বা ত্রুটির মার্জিন এর চেয়ে ছোট এটি নির্দেশ করবে যে ফলাফলগুলি এখন মোট জনসংখ্যার প্রকৃত উপস্থাপনার নিকটে এবং এটি জরিপটি যে পর্যবেক্ষণের বিষয়ে একটি উচ্চ স্তরের আস্থা তৈরি করবে।