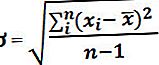এক্সেলের মধ্যে NORM.S.INV ফাংশন (সূত্র, উদাহরণ) | কিভাবে ব্যবহার করে?
সূত্রের নাম হিসাবে, আমরা ভাবতে পারি যে এই ফাংশনটি সাধারণ বিতরণের বিপরীত গণনা করে এবং এই ফাংশনের জন্য, ডেটা সেটের গড়টি সর্বদা শূন্য থাকে এবং মান বিচ্যুতি সর্বদা এক থাকে, এটি এক্সেলের একটি অন্তর্নির্মিত ফাংশনও বটে যা পরিসংখ্যান বিশ্লেষণের মতো পরিসংখ্যানগুলিতে ব্যবহৃত হয়।
এক্সরেলে NORM.S.INV () ফাংশন
এটি এক্সেলের একটি প্রাক-বিল্ট ইন্টিগ্রেটেড ফাংশন যা এক্সেলে স্ট্যাটিস্টিকাল ফাংশনগুলির অধীনে শ্রেণিবদ্ধ করা হয়। NORM.S.INV এক্সেল ফাংশনটি এই এক্সেল ফাংশনের পুরানো সংস্করণের তুলনায় উন্নত নির্ভুলতার সাথে সর্বশেষ আপডেট হওয়া সংস্করণ

- সাধারণ বিতরণ পরিসংখ্যানগুলিতে সর্বাধিক ব্যবহৃত বিতরণ। একে "বেল বাঁক" বা "গাউসিয়ান বক্ররেখা" হিসাবেও ডাকা হয়
- সাধারণ বিতরণটি তার গড় এবং স্ট্যান্ডার্ড বিচ্যুতির (এসডি) মানের উপর ভিত্তি করে পুরোপুরি বর্ণিত হতে পারে।
- একটি সাধারণ বিতরণকে স্ট্যান্ডার্ড নরমাল ডিস্ট্রিবিউশন বলা হয় যখন এর গড় মান "0" বা শূন্য হয় এবং মান বিচ্যুতির মান 1 এর সমান হয়
সাধারণ বিতরণটি নীচে উল্লিখিত সূত্রটি ব্যবহার করে মানক করা যেতে পারে
z = (x - গড়) / এসডি

এক্স-অক্ষের জেড মান হ'ল মানক বিচ্যুতি। এখানে, বক্ররেখের রেড তীরযুক্ত রেখাটি নির্দেশ করে যেখানে গড় মানের স্ট্যান্ডার্ড বিচ্যুতিটি 1 এর মধ্যে রয়েছে, যেখানে বক্ররেখায় সবুজ তীরযুক্ত রেখাটি নির্দেশ করে যেখানে 0 মীণ মানের মান বিচ্যুতি 2 এর মধ্যে রয়েছে।
NORM.S.INV এক্সেল ফাংশন সংজ্ঞা
NORM.S.INV এক্সেল ফাংশন প্রদত্ত সম্ভাব্যতার মানটির জন্য বিপরীতমুখী সাধারণ ক্রমবর্ধমান বিতরণ সন্ধান বা গণনা করতে ব্যবহৃত হয়
এটি স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণের বিপরীতটি প্রদান করে। বিতরণটির শূন্যের গড় এবং একটির একটি মানক বিচ্যুতি রয়েছে।
একটি পরিবর্তনশীল গড়ের নির্দিষ্ট দূরত্বে থাকা সম্ভাবনাটি প্রদত্ত, এটি z মান (মানক আদর্শ বিচ্যুত) গণনা করে, যেখানে এটি বক্ররেখার অধীনে একটি অঞ্চলের সাথে সম্পর্কিত
সাধারণত, ক্ষেত্রফল 0 এবং এর মধ্যে হওয়া উচিত
এখানে z মান (স্ট্যান্ডার্ড নরমাল বিচ্যুতি), এক-লেজযুক্ত সম্ভাবনার পি এর সাথে মিলে যায়।
যেখানে পি মান 0 এবং 1 (0) এর মধ্যে হতে হবে<>
এক্সেলে NORM.S.INV সূত্র
মাইক্রোসফ্ট এক্সেলের NORM.S.INV ফাংশনের সিনট্যাক্স বা সূত্রটি হ'ল:

এটির বাক্য গঠন বা সূত্রের নীচে বর্ণিত যুক্তি রয়েছে:
সম্ভাবনা: (বাধ্যতামূলক বা প্রয়োজনীয় প্যারামিটার) এটি সাধারণ বিতরণের সাথে সম্পর্কিত একটি সম্ভাবনা
এটি NORM.S.DIST ফাংশনের বিপরীত
এক্সেলে NORM.S.INV ফাংশনটি কীভাবে ব্যবহার করবেন?
NORM.S.INV এক্সেল কার্যটি এক্সেলে কীভাবে কাজ করে তা দেখা যাক।
আপনি এক্সেল এ এই NORM.S.INV ফাংশনটি ডাউনলোড করতে পারেন - এক্সেলের NORM.S.INV ফাংশনউদাহরণ # 1 - একটি সম্ভাবনার জন্য (পি) মান 0.5 এর চেয়ে কম
নীচে উল্লিখিত উদাহরণে, আমার একটি সেল "C9" i.e.0.28 এ একটি ডেটাसेट রয়েছে, যা সম্ভাবনার মান।

এখানে আমাকে NORM.S.INV এক্সেল ফাংশন ব্যবহার করে স্ট্যান্ডার্ড স্বাভাবিক ক্রমবর্ধমান বিতরণের বিপরীতটির আনুমানিক মান খুঁজে বের করতে হবে
আসুন সেল "C13" এ এই ফাংশনটি প্রয়োগ করি। “C13” ঘরটি নির্বাচন করুন

সূত্র সরঞ্জামদণ্ডের নীচে সন্নিবেশ ফাংশন বোতামটি (এফএক্স) ক্লিক করুন।

একটি সংলাপ বাক্স উপস্থিত হবে,

একটি ক্রিয়া বাক্স অনুসন্ধানে "NORM" শব্দটি টাইপ করুন, বিভিন্ন স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ সমীকরণ উপস্থিত হয়। এতে NORM.S.INV এক্সেল ফাংশনটি নির্বাচন করুন

সম্ভাবনা: এটি সাধারণ বিতরণের সাথে সম্পর্কিত একটি সম্ভাবনা, এখানে এটি 0.28

সম্ভাব্যতা যুক্তিটি প্রবেশ করার পরে ঠিক আছে ক্লিক করুন = NORM.S.INV (0.28)

এটি স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ বা স্ট্যান্ডার্ডাইজড নর্মাল বিচ্যুতির বিপরীতটির আনুমানিক মানটি প্রত্যাবর্তন করে -0.582841507

উদাহরণ # 2 - সম্ভাব্যতার জন্য (পি) মান 0.5 এরও বেশি
নীচে উল্লিখিত উদাহরণে, আমার একটি কক্ষ “B22” i.e.0.88 এ একটি ডেটাসেট রয়েছে, যা সম্ভাবনার মান।

এখানে আমাকে NORMSINV () ফাংশন ব্যবহার করে স্ট্যান্ডার্ড স্বাভাবিক ক্রমবর্ধমান বিতরণের বিপরীতটির আনুমানিক মান খুঁজে বের করতে হবে
আসুন সেল "বি 26" এ এই ফাংশনটি প্রয়োগ করি। “B26” ঘরটি নির্বাচন করুন

সূত্র সরঞ্জামদণ্ডের নীচে সন্নিবেশ ফাংশন বোতামটি (এফএক্স) ক্লিক করুন।

একটি ডায়লগ বক্স প্রদর্শিত হবে।

একটি ক্রিয়া বাক্স অনুসন্ধানে "NORM" শব্দটি টাইপ করুন, বিভিন্ন স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ সমীকরণ উপস্থিত হয়। এতে NORM.S.INV () ফাংশনটি নির্বাচন করুন।

ফাংশনে ডাবল ক্লিক করুন, একটি ডায়ালগ বাক্স উপস্থিত হবে যেখানে আর্গুমেন্টগুলি পূরণ করা বা প্রবেশ করা প্রয়োজন অর্থাত্ = NORM.S.INV (সম্ভাব্যতা)
সম্ভাবনা: এটি সাধারণ বিতরণের সাথে সম্পর্কিত সম্ভাবনা, এখানে এটি 0.88

সম্ভাব্যতা যুক্তি যুক্ত করার পরে ঠিক আছে ক্লিক করুন, যেমন = NORM.S.INV (0.88)

এটি স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ বা স্ট্যান্ডার্ডাইজড নর্মাল বিচ্যুতির অর্থাত্ 1.174986792 এর বিপরীতটির আনুমানিক মানটি প্রদান করে

উদাহরণ # 3 - একটি সম্ভাব্যতার জন্য (পি) 0.51 এর মান
নীচে উল্লিখিত উদাহরণে আমার একটি ঘরে "বি 32" অর্থাৎ 0.51 তে একটি ডেটাসেট রয়েছে যা সম্ভাবনার মান।

এখানে আমাকে NORM.S.INV () ফাংশন ব্যবহার করে স্ট্যান্ডার্ড স্বাভাবিক ক্রমবর্ধমান বিতরণের বিপরীতটির আনুমানিক মান খুঁজে বের করতে হবে
আসুন সেল "বি 37" এ এই ফাংশনটি প্রয়োগ করি।

সূত্র সরঞ্জামদণ্ডের নীচে সন্নিবেশ ফাংশন বোতামটি (এফএক্স) ক্লিক করুন

একটি সংলাপ বাক্স উপস্থিত হবে।

একটি ক্রিয়া বাক্স অনুসন্ধানে "NORM" শব্দটি টাইপ করুন, বিভিন্ন স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ সমীকরণ উপস্থিত হয়।

সম্ভাবনা: এটি সাধারণ বিতরণের সাথে সম্পর্কিত একটি সম্ভাবনা, এখানে এটি 0.5 is

সম্ভাব্যতা যুক্তিটি প্রবেশ করার পরে ঠিক আছে ক্লিক করুন = NORM.S.INV (0.51)

এটি স্ট্যান্ডার্ড সাধারণ ক্রমবর্ধমান বিতরণ বা স্ট্যান্ডার্ডাইজড নর্মাল বিচ্যুতির বিপরীতটির আনুমানিক মান ফেরৎ দেয় 0.025068908

এক্সেলের NORMSINV () ফাংশন সম্পর্কে মনে রাখার বিষয়গুলি
এই ক্রিয়াকলাপে ঘটে যাওয়া এক্সেলের বেশিরভাগ সাধারণ ত্রুটি হ'ল #NUM! ত্রুটি & # ভ্যালু! ত্রুটি
1. #NUM! ত্রুটি
#NUM! ত্রুটি ঘটে যখন প্রদত্ত সম্ভাব্যতা যুক্তি শূন্যের চেয়ে কম (নেতিবাচক মান) বা শূন্যের সমান বা একের বেশি হয়।
নীচে উল্লিখিত টেবিলটিতে, ঘর "B41" মান সংখ্যা 0, আমরা যদি NORM.S.INV ফাংশনটি প্রয়োগ করি তবে এটি একটি #NUM প্রদান করে! ত্রুটি

একইভাবে, আমরা যদি প্রয়োগ করি, N42M.S.INV () B42 এবং B43 কোষে 1.5 এবং -1.5 মানগুলিতে ফাংশন করে, এটি একটি ফিরে আসে #NUM! ত্রুটি

২. # মান! ত্রুটি
# মূল্য! ত্রুটি দেখা দেয় যদি প্রদত্ত কোনও আর্গুমেন্ট পাঠ্য মান বা অ-সংখ্যাযুক্ত হয়
নীচে উল্লিখিত সারণীতে, ঘর "বি 24" এর পাঠ্যের মান রয়েছে অর্থাত্ এতে "পাঠ্য" শব্দটি রয়েছে। যদি আমরা স্ট্যান্ডার্ড স্বাভাবিক ক্রমবর্ধমান বিতরণের বিপরীতটির আনুমানিক মান খুঁজে পেতে NORM.S.INV এক্সেল ফাংশনটি প্রয়োগ করি। এটি #VALUE ফেরত দেয়! ত্রুটি

এই ফাংশন মানগুলির যথার্থতা বা নির্ভুলতা NORM.S.INV এবং NORM.S.DIST এর যথার্থতার উপর নির্ভর করে। মান। এটি একটি পুনরাবৃত্তি অনুসন্ধান কৌশল ব্যবহার করে।