নমুনা আকার (সংজ্ঞা, সূত্র) | নমুনা আকার গণনা করুন
জনসংখ্যার নমুনা আকার নির্ধারণের সূত্র
নমুনা আকার সূত্রটি আস্থার স্তর এবং ত্রুটির প্রান্তের পাশাপাশি জনসংখ্যার পর্যাপ্ত বা সঠিক অনুপাত জানতে প্রয়োজনীয় ন্যূনতম নমুনা আকার গণনা বা নির্ধারণে সহায়তা করে।
"নমুনা" শব্দটি জনসংখ্যার সেই অংশকে বোঝায় যা জনসংখ্যা সম্পর্কে অনুমানগুলি আঁকতে সক্ষম করে এবং তাই গুরুত্বপূর্ণ যে নমুনার আকারটি পর্যাপ্ত পর্যাপ্ত যাতে অর্থবোধক সূত্রগুলি তৈরি করা যায়। অন্য কথায়, এটি ত্রুটি এবং আত্মবিশ্বাসের স্তরের প্রয়োজনীয় মার্জিনের সাথে প্রকৃত জনসংখ্যার অনুপাতটি অনুমান করার জন্য এটি ন্যূনতম আকার। এর মতো, পরিসংখ্যান বিশ্লেষণে যথাযথ নমুনা আকারের নির্ধারণ হ'ল পুনরাবৃত্তি সমস্যাগুলির মধ্যে একটি। এর সমীকরণটি জনসংখ্যার আকার, সাধারণ বিতরণের সমালোচনামূলক মান, নমুনা অনুপাত এবং ত্রুটির মার্জিন ব্যবহার করে উদ্ভূত হতে পারে।
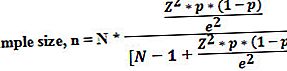

কোথায়,
- এন = জনসংখ্যার আকার,
- জেড = প্রয়োজনীয় আস্থা স্তরে সাধারণ বিতরণের সমালোচনা মান,
- p = নমুনা অনুপাত,
- e = ত্রুটির মার্জিন
নমুনা আকার গণনা কিভাবে? (ধাপে ধাপে)
- ধাপ 1: প্রথমত, জনসংখ্যার আকার নির্ধারণ করুন যা আপনার জনসংখ্যার স্বতন্ত্র সত্তার মোট সংখ্যা এবং এটি এন দ্বারা চিহ্নিত করা হয়েছে। [দ্রষ্টব্য: ক্ষেত্রে, জনসংখ্যার আকার খুব বড় তবে সঠিক সংখ্যাটি জানা যায়নি, তবে নমুনাটি ব্যবহার করুন কারণ নমুনাটি এর চেয়ে বড় জনগোষ্ঠীর জন্য আকার খুব বেশি পরিবর্তন করে না]]
- ধাপ ২: এরপরে প্রয়োজনীয় আস্থা স্তরে সাধারণ বিতরণের সমালোচনামূলক মান নির্ধারণ করুন। উদাহরণস্বরূপ, 95% আত্মবিশ্বাস স্তরের সমালোচনামূলক মানটি 1.96।
- ধাপ 3: এরপরে, নমুনা অনুপাত নির্ধারণ করুন যা পূর্ববর্তী সমীক্ষার ফলাফল থেকে ব্যবহার করা যেতে পারে বা একটি ছোট পাইলট জরিপ চালিয়ে সংগ্রহ করা যেতে পারে। [দ্রষ্টব্য: যদি অনিশ্চিত হয় যে সর্বদা রক্ষণশীল পদ্ধতির হিসাবে 0.5 ব্যবহার করতে পারে এবং এটি সর্বাধিক সম্ভাব্য নমুনার আকার দেবে]]
- পদক্ষেপ 4: এরপরে, ত্রুটির মার্জিন নির্ধারণ করুন যা প্রকৃত জনসংখ্যা মিথ্যা বলে প্রত্যাশা করা হয়েছে range. [দ্রষ্টব্য: ত্রুটির প্রান্তটি আরও ছোট, আরও যথার্থ এবং তাই সঠিক উত্তর]]
- পদক্ষেপ 5: পরিশেষে, জনসংখ্যার আকার (পদক্ষেপ 1), প্রয়োজনীয় আত্মবিশ্বাসের স্তরে (সাধারণ পদক্ষেপ 2), নমুনার অনুপাত (ধাপ 3) এবং ত্রুটির মার্জিন (ধাপ 4) হিসাবে সাধারণ বিতরণের সমালোচনামূলক মান ব্যবহার করে নমুনা আকারের সমীকরণটি উত্পন্ন হতে পারে নিচে দেখানো.
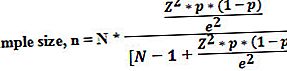
উদাহরণ
আপনি এই নমুনা আকার সূত্র এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - নমুনা আকারের সূত্র এক্সেল টেম্পলেটউদাহরণ # 1
আসুন আমরা এমন একজন খুচরা বিক্রেতার উদাহরণ গ্রহণ করি যিনি তাদের নির্দিষ্ট গ্রাহকরা নির্দিষ্ট দিনে তাদের ওয়েবসাইট দেখার পরে তাদের কতজন গ্রাহক তাদের কাছ থেকে কোনও আইটেম কিনেছিলেন তা জানতে আগ্রহী। দেওয়া হয়েছে যে তাদের ওয়েবসাইটটিতে প্রতিদিন গড়ে 10,000 টি মতামত রয়েছে, গ্রাহকদের নমুনার আকার নির্ধারণ করুন যে তাদের ত্রুটির 5% মার্জিনের সাথে একটি 95% আত্মবিশ্বাস স্তরে পর্যবেক্ষণ করতে হবে যদি:
- তারা বর্তমান রূপান্তর হার সম্পর্কে অনিশ্চিত।
- তারা পূর্ববর্তী সমীক্ষা থেকে জানে যে রূপান্তর হার 5%।
দেওয়া,
- জনসংখ্যার আকার, এন = 10,000
- 95% আত্মবিশ্বাস স্তরের সমালোচনামূলক মান, জেড = 1.96
- ত্রুটির মার্জিন, ই = 5% বা 0.05
1 - যেহেতু বর্তমান রূপান্তর হারটি অজানা, তাই আসুন আমরা পি = 0.5 অনুমান করি
সুতরাং, সূত্রটি ব্যবহার করে নমুনার আকারটি গণনা করা যেতে পারে,
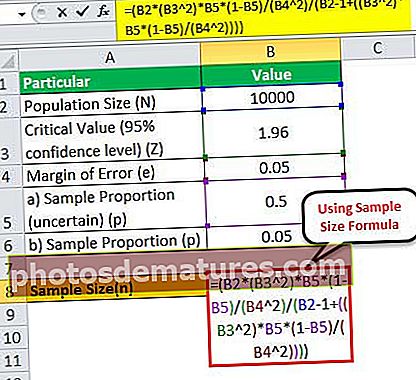
= (10,000 * (1.96 2)*0.5*(1-0.5)/(0.05 2)/(10000 – 1+((1.96 2)* 0.5*(1-0.5)/(0.05 2))))
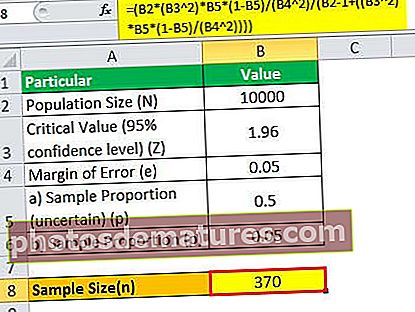
সুতরাং, 370 গ্রাহকরা অর্থবহ অনুমান অর্জনের জন্য পর্যাপ্ত হবে।
2 - বর্তমান রূপান্তর হার পি = 5% বা 0.05
সুতরাং উপরের সূত্রটি ব্যবহার করে নমুনার আকারটি গণনা করা যেতে পারে,
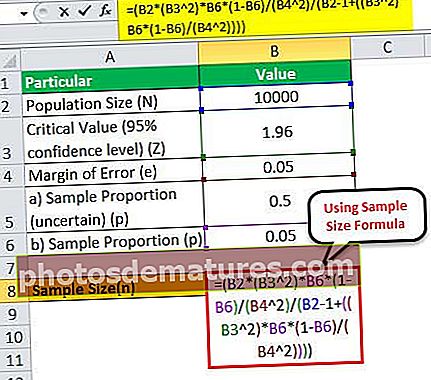
= (10,000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(10000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
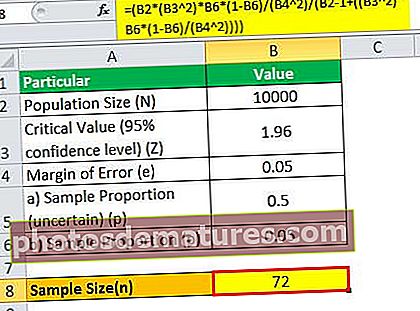
অতএব, এক্ষেত্রে 72২ জন গ্রাহক অর্থবহ অনুমানের পক্ষে যথেষ্ট হবে।
উদাহরণ # 2
আসুন আমরা উপরের উদাহরণটি নিই এবং এই ক্ষেত্রে আসুন আমরা ধরে নিই যে জনসংখ্যার আকার, অর্থাৎ দৈনিক ওয়েবসাইটের ভিউ, 100,000 থেকে 120,000 এর মধ্যে, তবে তার সঠিক মানটি জানা যায় না। বাকী মানগুলি 5% রূপান্তর হারের সাথে একই। 100,000 এবং 120,000 উভয়ের জন্য নমুনার আকার গণনা করুন।
দেওয়া,
- নমুনা অনুপাত, পি = 0.05
- 95% আত্মবিশ্বাস স্তরের সমালোচনামূলক মান, জেড = 1.96
- ত্রুটির মার্জিন, ই = 0.05
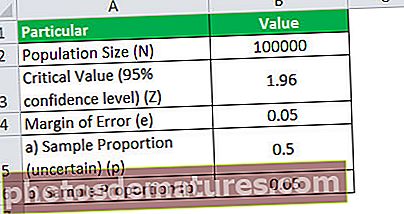
সুতরাং, এন = 100,000 এর জন্য নমুনার আকার হিসাবে গণনা করা যেতে পারে,
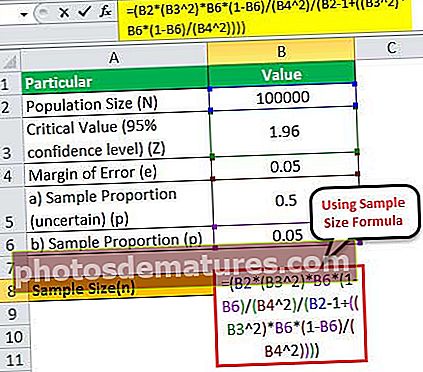
= (100000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(100000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
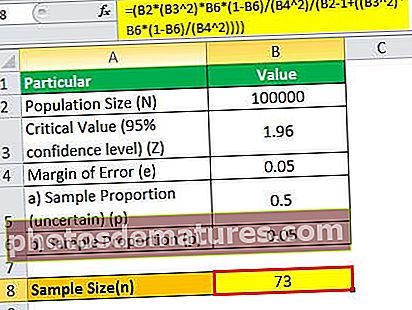
সুতরাং, N = 120,000 এর জন্য নমুনার আকার হিসাবে গণনা করা যেতে পারে,
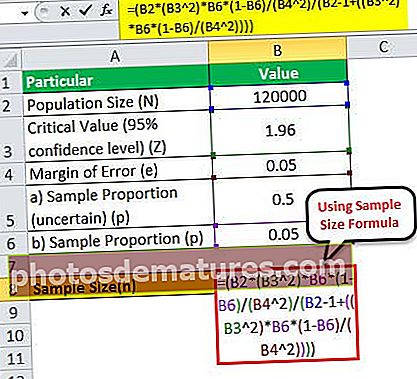
= (120000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(120000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))
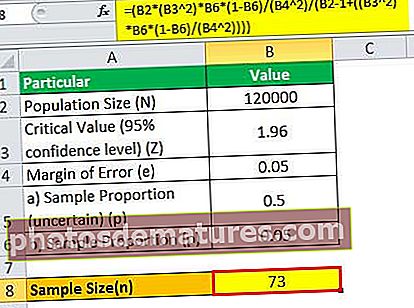
সুতরাং, এটি প্রমাণিত হয়েছে যেহেতু জনসংখ্যার আকারটি খুব বড় হতে চলেছে, এটি নমুনার আকারের গণনায় অপ্রাসঙ্গিক হয়ে ওঠে।
প্রাসঙ্গিকতা এবং ব্যবহার
নমুনা আকারের গণনা যথাযথ নমুনা আকারের ধারণাটি বোঝা গুরুত্বপূর্ণ কারণ এটি গবেষণার ফলাফলগুলির বৈধতার জন্য ব্যবহৃত হয়। যদি এটি খুব ছোট হয় তবে এটি কার্যকর ফলাফল দেয় না, যখন একটি নমুনা খুব বড় হয় তবে অর্থ এবং সময় উভয়ই নষ্ট হতে পারে। পরিসংখ্যানগতভাবে, উল্লেখযোগ্য নমুনার আকারটি মূলত বাজার গবেষণা সমীক্ষা, স্বাস্থ্যসেবা জরিপ এবং শিক্ষা সমীক্ষার জন্য ব্যবহৃত হয়।