আর স্কোয়ার্ড (আর ^ 2) - সংজ্ঞা, সূত্র, গণনা আর স্কোয়ার
রিগ্রেশনে আর স্কোয়ার (আর 2) কী?
আর-স্কোয়ার্ড (আর 2) একটি গুরুত্বপূর্ণ পরিসংখ্যান পরিমাপ যা একটি রিগ্রেশন মডেল যা নির্ভরশীল ভেরিয়েবলের জন্য পরিসংখ্যানগত পদগুলির মধ্যে পার্থক্য বা তারতম্যের অনুপাতকে উপস্থাপন করে যা একটি স্বাধীন ভেরিয়েবল বা ভেরিয়েবল দ্বারা ব্যাখ্যা করা যেতে পারে। সংক্ষেপে, এটি নির্ধারণ করে যে কতটা ভাল ডাটা রিগ্রেশন মডেলকে ফিট করবে।
স্কোয়ার্ড ফর্মুলা
আর স্কোয়ারের গণনার জন্য আপনাকে সহাবন্ধিক সহগ নির্ধারণ করতে হবে এবং তারপরে আপনাকে ফলাফলটি বর্গাকার করতে হবে।
আর স্কোয়ার্ড ফর্মুলা = আর 2
যেখানে পারস্পরিক সম্পর্ক সহগ নীচে প্রতি গণনা করা যেতে পারে:
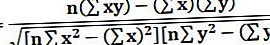
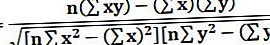
কোথায়,
- r = সংযোগ সহগ
- প্রদত্ত ডেটাসেটে n = সংখ্যা
- x = প্রসঙ্গে প্রথম পরিবর্তনশীল
- y = দ্বিতীয় পরিবর্তনশীল
ব্যাখ্যা
যদি সেই দুটি ভেরিয়েবলের মধ্যে লিনিয়ার বা অ-রৈখিক হতে পারে এমন কোনও সম্পর্ক বা পারস্পরিক সম্পর্ক থাকে তবে এটি যদি স্বতন্ত্র ভেরিয়েবলের মানতে পরিবর্তন হয় তবে তা চিহ্নিত করতে পারে, তবে অন্যান্য নির্ভরশীল ভেরিয়েবল সম্ভবত রৈখিক বা অ- রৈখিক
সূত্রের সংখ্যার অংশটি পরীক্ষা করে যে তারা একসাথে চলে এবং তাদের পৃথক গতিবিধি এবং তাদের উভয় একত্রে চলার তুলনামূলক শক্তি অপসারণ করে এবং সূত্রের ডোনমিনেটর অংশটি পার্থক্যের পণ্যের বর্গমূল গ্রহণ করে অঙ্ককে স্কেল করে তাদের স্কোয়ার ভেরিয়েবল থেকে ভেরিয়েবল। এবং আপনি যখন এই ফলাফলটি স্কোয়ার করলেন তখন আমরা আর স্কোয়ার পেয়ে যা যা দৃ determination়সংকল্পের সহগ ছাড়া কিছুই নয়।
উদাহরণ
আপনি এই আর স্কোয়ারড ফর্মুলা এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - আর স্কোয়ারড ফর্মুলা এক্সেল টেম্পলেটউদাহরণ # 1
নিম্নলিখিত দুটি ভেরিয়েবল x এবং y বিবেচনা করুন, আপনাকে রিগ্রেশন-এ আর স্কোয়ার্ড গণনা করতে হবে।

সমাধান:
উপরে উল্লিখিত সূত্রটি ব্যবহার করে, আমাদের প্রথমে পারস্পরিক সম্পর্ক সহগকে গণনা করতে হবে।

আমাদের উপরের টেবিলের n = 4 সহ সমস্ত মান রয়েছে।
আসুন চিত্রটিতে পৌঁছানোর জন্য সূত্রের মানগুলি ইনপুট করি।

আর = (4 * 26,046.25) - (265.18 * 326.89) / √ [(4 * 21,274.94) - (326.89) 2] * [(4 * 31,901.89) - (326.89) 2]
আর = 17,501.06 / 17,512.88
সম্পর্কযুক্ত সহগ হবে-

r = 0.99932480
সুতরাং, গণনাটি নিম্নরূপ হবে,

আর 2 = (0.99932480) 2
রিগ্রেশনে আর স্কোয়ারড ফর্মুলা

আর 2 = 0.998650052
উদাহরণ # 2
অপরিশোধিত তেলের দামের পরিবর্তনগুলি তার রুপির মূল্যকে প্রভাবিত করেছে কিনা তা ভারত একটি উন্নয়নশীল দেশ স্বাধীন বিশ্লেষণ করতে চায়। নীচে প্রতি বছর ধরে গড়ে গড়ে ডলারের বিপরীতে ব্রেন্ট অপরিশোধিত তেলের দাম এবং রুপির মূল্যায়ন উভয়ের ইতিহাস নীচে রয়েছে।

ভারতের কেন্দ্রীয় ব্যাংক আরবিআই পরবর্তী সভায় আপনার কাছে এটির উপস্থাপনা দেওয়ার জন্য যোগাযোগ করেছে। নির্ধারণ করুন যে অপরিশোধিত তেলের চলাচল প্রতি ডলারের টাকায় চলাচলকে প্রভাবিত করে?
সমাধান:
উপরের পারস্পরিক সম্পর্কের সূত্রটি ব্যবহার করে আমরা প্রথমে পারস্পরিক সম্পর্কের সহগকে গণনা করতে পারি। একের পরিবর্তক হিসাবে সিদ্ধ হয়ে ওঠার অপরিশোধিত তেলের দাম এবং অন্য ডলার হিসাবে রুপিকে y হিসাবে অন্য পরিবর্তনশীল হিসাবে বিবেচনা করা।

আমাদের উপরের টেবিলের n = 6 সহ সমস্ত মান রয়েছে।
আসুন চিত্রটিতে পৌঁছানোর জন্য সূত্রের মানগুলি ইনপুট করি।

আর = (6 * 23592.83) - (356.70 * 398.59) / √ [(6 * 22829.36) - (356.70) 2] * [(6 * 26529.38) - (398.59) 2]
আর = -620.06 / 1,715.95
সম্পর্কযুক্ত সহগ হবে-

r = -0.3614
সুতরাং, গণনাটি নিম্নরূপ হবে,

r2 = (-0.3614) 2
রিগ্রেশনে স্কোয়ার্ড ফর্মুলা

আর 2 = 0.1306
বিশ্লেষণ: এটি প্রদর্শিত হয় যে অপরিশোধিত তেলের দামের পরিবর্তন এবং ভারতীয় রুপির দামের পরিবর্তনের মধ্যে একটি সামান্য সম্পর্ক রয়েছে। অপরিশোধিত তেলের দাম বাড়ার সাথে সাথে ভারতীয় রুপির পরিবর্তনগুলিও প্রভাবিত করে। তবে যেহেতু আর স্কোয়ারটি কেবল ১৩%, তারপরে অপরিশোধিত তেলের দামের পরিবর্তনগুলি ভারতীয় রুপির পরিবর্তন সম্পর্কে খুব কম ব্যাখ্যা করে এবং ভারতীয় রুপিকে অন্যান্য ভেরিয়েবলের পরিবর্তনেরও সাপেক্ষে যার জন্য দায়বদ্ধ হওয়া দরকার।
উদাহরণ # 3
এক্সওয়াইজেড পরীক্ষাগার উচ্চতা এবং ওজন নিয়ে গবেষণা পরিচালনা করছে এবং এই ভেরিয়েবলগুলির মধ্যে কোনও ধরণের সম্পর্ক রয়েছে কিনা তা জানতে আগ্রহী। প্রতিটি বিভাগের জন্য 5000 জনের একটি নমুনা সংগ্রহ করার পরে এবং সেই নির্দিষ্ট গোষ্ঠীর গড় ওজন এবং গড় উচ্চতা নিয়ে এসেছিল।
নীচে তারা জড়ো করা বিবরণ দেওয়া আছে।

আপনাকে আর স্কোয়ার্ড গণনা করতে হবে এবং উপসংহারে আসতে হবে যদি এই মডেলটি উচ্চতার বৈচিত্রগুলি ওজনের বিভিন্নতাগুলিকে প্রভাবিত করে explains
সমাধান:
উপরের পারস্পরিক সম্পর্কের সূত্রটি ব্যবহার করে আমরা প্রথমে পারস্পরিক সম্পর্ক সহগকে গণনা করতে পারি। এক্সকে বলুন উচ্চতার সাথে চিকিত্সা করা এবং ওজনকে y হিসাবে অন্য পরিবর্তনশীল হিসাবে বিবেচনা করা।

আমাদের উপরের টেবিলের n = 6 সহ সমস্ত মান রয়েছে।
আসুন চিত্রটিতে পৌঁছানোর জন্য সূত্রের মানগুলি ইনপুট করি।

আর = (7 * 74,058.67) - (1031 * 496.44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793.59) - (496.44) 2]
আর = 6,581.05 / 7,075.77
সম্পর্কযুক্ত সহগ হবে-

সম্পর্কের সহগ (আর) = 0.930
সুতরাং, গণনাটি নিম্নরূপ হবে,

r2 = 0.865
বিশ্লেষণ: পারস্পরিক সম্পর্ক ইতিবাচক, এবং উচ্চতা এবং ওজনের মধ্যে কিছু সম্পর্ক রয়েছে বলে উচ্চতা ব্যক্তির ওজন বাড়িয়ে তোলে বলেও মনে হয় increased যদিও আর 2 প্রস্তাব দেয় যে ওজনের পরিবর্তনের জন্য উচ্চতার গুণাবলীতে 86% পরিবর্তন এবং 14% অব্যক্ত নয়।
প্রাসঙ্গিকতা এবং ব্যবহার
নিঃসন্দেহে স্কোয়ার আর এর প্রাসঙ্গিকতা হ'ল প্রদত্ত ভবিষ্যদ্বাণীকৃত ফলাফল বা ফলাফলগুলির মধ্যে ঘটে যাওয়া ভবিষ্যতের ঘটনাগুলির সম্ভাব্যতা খুঁজে পাওয়ার ক্ষমতা। যদি মডেলটিতে আরও নমুনা যুক্ত করা হয়, তবে সহগগুলি নতুন পয়েন্ট বা নতুন ডেটাসেটের লাইনে পড়ার সম্ভাবনা বা সম্ভাবনা দেখায়। উভয় ভেরিয়েবলের দৃ strong় সংযোগ থাকলেও সংকল্পটি কার্যকারণ প্রমাণ করে না।
আর স্কোয়ারের বেশিরভাগ জায়গাগুলি মিউচুয়াল ফান্ডের পারফরম্যান্স ট্র্যাকিংয়ের জন্য, হেজ ফান্ডগুলির ঝুঁকি ট্র্যাকিংয়ের জন্য, বাজারের সাথে স্টক কতটা ভাল চলছে তা নির্ধারণ করার জন্য, যেখানে স্টোরের গতিবিধি কতটা ব্যাখ্যা করা যেতে পারে তা আর 2 বলে দেয় বাজারে আন্দোলন দ্বারা।