টি বিতরণের সূত্র | শিক্ষার্থীদের টি বিতরণ গণনা করুন | উদাহরণ
শিক্ষার্থীদের টি বিতরণ গণনা করার সূত্র
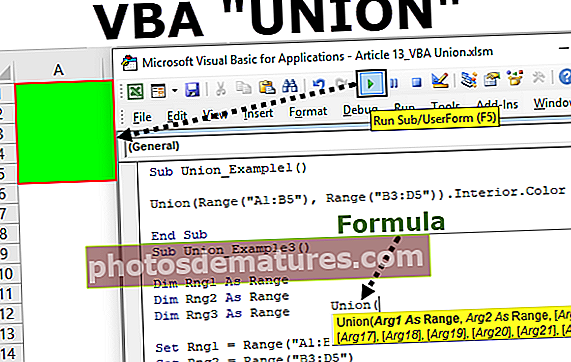
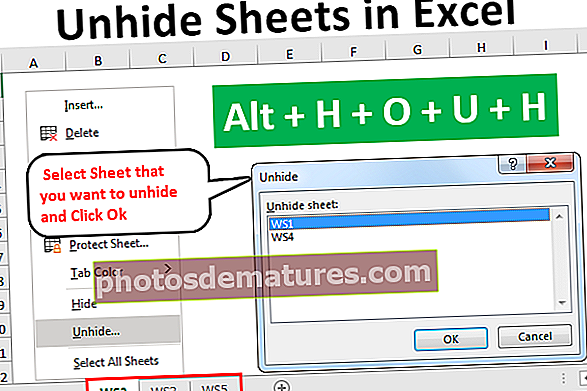
টি ডিস্ট্রিবিউশন গণনা করার সূত্রটি (যা জনপ্রিয়ভাবে শিক্ষার্থীদের টি বিতরণ হিসাবেও পরিচিত) নমুনার গড় (প্রথম নমুনার অর্থ) থেকে জনসংখ্যার গড় (প্রথম নমুনার গড়) বাদ দিয়ে দেখানো হয়েছে যা [এক্স-বার - μ] যা এরপরে অর্থের প্রমিত বিচ্যুতি দ্বারা বিভক্ত হয় যা প্রাথমিকভাবে n এর বর্গমূল দ্বারা বিভক্ত হয় যা সেই নমুনায় [s ÷ √ (n)] এর একক সংখ্যা।
টি ডিস্ট্রিবিউশন হ'ল এক ধরণের বিতরণ যা দেখতে প্রায় সাধারণ বন্টন বক্র বা বেল বক্রর মতো তবে কিছুটা মোটা এবং খাটো লেজযুক্ত। যখন নমুনার আকার ছোট হয় তখন এই বিতরণটি সাধারণ বিতরণের পরিবর্তে ব্যবহৃত হবে।


কোথায়,
- x̄ নমুনা গড়
- μ হ'ল জনসংখ্যা গড়
- গুলি হ'ল মানক বিচ্যুতি
- n প্রদত্ত নমুনার আকার
টি বিতরণের গণনা
শিক্ষার্থীর টি বিতরণের গণনা বেশ সহজ তবে হ্যাঁ, মানগুলি প্রয়োজন। উদাহরণস্বরূপ, একজনের প্রয়োজন জনসংখ্যার অর্থ যা মহাবিশ্ব, যা জনসংখ্যার গড় ব্যতীত কিছুই নয়, যখন জনসংখ্যার সত্যতা পরীক্ষা করার জন্য নমুনা গড়ের প্রয়োজন হয় অর্থ জনসংখ্যার ভিত্তিতে দাবি করা বক্তব্যটি সত্যই সত্য কিনা এবং যদি নেওয়া হয় তবে নমুনা একই বিবৃতি উপস্থাপন করবে। সুতরাং, টি-টি বিতরণ সূত্রটি জনসংখ্যার গড় থেকে নমুনা গড়কে বিয়োগ করে এবং তারপরে মানটিকে মানিক করে তোলার জন্য এটি স্ট্যান্ডার্ড বিচ্যুতির মাধ্যমে ভাগ করে এবং নমুনার আকারের বর্গমূলের সাথে গুণ করে।
তবে, যেহেতু টি বিতরণ গণনার কোনও সীমা নেই তাই মানটি অদ্ভুত হতে পারে এবং আমরা ছাত্রদের টি বিতরণে একটি মান পৌঁছানোর সীমাবদ্ধতা থাকায় সম্ভাব্যতা গণনা করতে পারব না এবং এটি কেবলমাত্র ছোট নমুনার আকারের জন্য কার্যকর। স্কোর এ পৌঁছানোর পরে সম্ভাব্যতা গণনা করার জন্য শিক্ষার্থীর টি বিতরণ টেবিল থেকে তার মান খুঁজে নেওয়া দরকার।
উদাহরণ
আপনি এই টি বিতরণ এক্সেল টেম্পলেটটি এখানে ডাউনলোড করতে পারেন - টি বিতরণ এক্সেল টেম্পলেটউদাহরণ # 1
নিম্নলিখিত ভেরিয়েবল আপনাকে দেওয়া হয় তা বিবেচনা করুন:
- জনসংখ্যা মানে = 310
- স্ট্যান্ডার্ড বিচ্যুতি = 50
- নমুনার আকার = 16
- নমুনা গড় = 290
টি-বিতরণ মান গণনা করুন।
সমাধান:
টি বিতরণের গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, টি বিতরণের গণনা নিম্নলিখিত হিসাবে করা যেতে পারে-
এখানে সমস্ত মান দেওয়া হয়েছে, আমাদের কেবল মানগুলি অন্তর্ভুক্ত করতে হবে।
আমরা টি বিতরণের সূত্রটি ব্যবহার করতে পারি


টি এর মান (290 - 310) / (50 / √16)

টি মান = -1.60
উদাহরণ # 2
এসআরএইচ সংস্থা দাবি করেছে যে বিশ্লেষক স্তরের তার কর্মীরা প্রতি ঘন্টা গড়ে $ 500 ডলার উপার্জন করে। বিশ্লেষক স্তরে ৩০ জন কর্মচারীর একটি নমুনা বাছাই করা হয় এবং প্রতি ঘন্টা তাদের গড় উপার্জন $ 450 এর নমুনা বিচ্যুতি সহ 450 ডলার এবং তাদের দাবি সত্য বলে ধরে নিয়ে টি-বিতরণ মান গণনা করুন যা টি এর সম্ভাব্যতা খুঁজে পাওয়ার জন্য ব্যবহৃত হবে - বিতরণ
সমাধান:
টি বিতরণের গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

সুতরাং, টি বিতরণের গণনা নিম্নলিখিত হিসাবে করা যেতে পারে-
এখানে সমস্ত মান দেওয়া হয়েছে, আমাদের কেবল মানগুলি অন্তর্ভুক্ত করতে হবে।
আমরা টি বিতরণের সূত্রটি ব্যবহার করতে পারি


টি এর মান (450 - 500) / (30 / √30)

টি মান = -9.13
সুতরাং টি স্কোরের মান -9.13
উদাহরণ # 3
ইউনিভার্সাল কলেজ বোর্ড এলোমেলোভাবে নির্বাচিত ৫০ জন অধ্যাপককে আইকিউ স্তরের পরীক্ষা দিয়েছিল। এবং এর থেকে তারা যে ফলাফলটি পেয়েছে তা হল গড় আইকিউ স্তরের স্কোরটি 121 এর বৈচিত্র সহ 120 ছিল। মনে করুন যে টি স্কোরটি 2.407। এই পরীক্ষার জন্য জনসংখ্যার অর্থ কী যা টি স্কোরের মানকে 2.407 হিসাবে ন্যায্যতা দেয়?
সমাধান:
টি বিতরণের গণনার জন্য নিম্নলিখিত ডেটা ব্যবহার করুন।

এখানে t টি মান সহ সমস্ত মান দেওয়া হয়েছে, আমাদের টি-এর পরিবর্তে এবার জনসংখ্যা গণনা করতে হবে।
আবার, আমরা উপলভ্য ডেটা ব্যবহার করব এবং নীচের সূত্রে প্রদত্ত মানগুলি সন্নিবেশ করে জনসংখ্যা মানে গণনা করব।
নমুনার গড়টি 120, জনসংখ্যার অর্থ অজানা, নমুনা স্ট্যান্ডার্ড বিচ্যুতিটি বৈকল্পিকের বর্গমূল হবে যা 11 হবে এবং নমুনার আকার 50 হবে।
সুতরাং, জনসংখ্যার গণনা মানে (μ) নিম্নলিখিত হিসাবে করা যেতে পারে-
আমরা টি বিতরণের সূত্রটি ব্যবহার করতে পারি


টি এর মান (120 - μ) / (11 / √50)
2.407 = (120 - μ) / (11 / √50)
-μ = -2.407 * (11 / √50) -120
জনসংখ্যা গড় (μ) হবে -

μ = 116.26
সুতরাং জনসংখ্যার গড় মূল্য হবে 116.26
প্রাসঙ্গিকতা এবং ব্যবহার
টি ডিস্ট্রিবিউশন (এবং সেই সাথে সম্পর্কিত টি স্কোরের মানগুলি) হাইপোথিসিস টেস্টিংয়ে ব্যবহৃত হয় যখন কোনওটি নাল হাইপোথিসিসকে প্রত্যাখ্যান করে বা গ্রহণ করতে হবে কিনা তা খুঁজে নেওয়া দরকার।

উপরের গ্রাফে, মধ্য অঞ্চলটি গ্রহণযোগ্যতা অঞ্চল এবং লেজ অঞ্চলটি প্রত্যাখ্যান অঞ্চল হবে। এই গ্রাফে যা 2 লেজযুক্ত পরীক্ষা, নীল শেডগুলি প্রত্যাখ্যান অঞ্চল হবে। লেজ অঞ্চলের অঞ্চলটি টি স্কোর বা জেড-স্কোর দিয়ে বর্ণিত হতে পারে। একটি উদাহরণ ধরুন, বাম দিকের চিত্রটি পাঁচ শতাংশের লেজের একটি অঞ্চল চিত্রিত করবে (যা উভয় পক্ষের 2.5%)। জেড-স্কোরটি 1.96 হওয়া উচিত (জেড-টেবিল থেকে মান গ্রহণ করা), যা গড় বা গড় থেকে 1.96 স্ট্যান্ডার্ড বিচ্যুতিকে উপস্থাপন করবে। Z স্কোরের মান -1.96 এর মানের চেয়ে কম বা জেড স্কোরের মান 1.96 এর চেয়ে বেশি হলে নাল অনুমানটি প্রত্যাখ্যান করা যায়।
সাধারণভাবে, এই বিতরণটি পূর্বের বর্ণিত হিসাবে ব্যবহৃত হবে যখন কারওর ছোট আকারের নমুনা আকার থাকে (বেশিরভাগ 30 বছরের কম) বা যদি কেউ না জানায় জনসংখ্যার বৈকল্পিকতা বা জনসংখ্যার মানক বিচ্যুতি কী। ব্যবহারিক উদ্দেশ্যগুলির জন্য (এটি আসল বিশ্বে রয়েছে), এটি সর্বদা প্রধানত থাকবে। প্রদত্ত নমুনার আকারটি যদি যথেষ্ট পরিমাণে বড় হয় তবে 2 টি বিতরণ কার্যত একই রকম হবে।